Net Present Value (NPV) - Discounted cash flow
Contents |
Abstract
Net Present Value (NPV) and Discounted Cash Flow (DCF) are two financial concepts, strongly connected to each other. So closely connected that the Net Present Value is a technique based on Discounted Cash Flows. [1] Both these concepts operate under the time value of money (TVM) principle, which assumes that money is worth more today than it is in the future. [1] When companies are making a project, program or portfolio investment decision, the NPV rule emerges as one of the of the most commonly used financial metrics.
On the one hand, Discounted Cash Flow (DCF) is a valuation method that estimates the attractiveness of an investment project or the value of a company based on their projected cash flows discounting them to the present. [2] [3] A DFC analysis involves forecasting future cash flows that a project or investment is expected to generate, and then discounting those values back to the present using a discount rate or required rate of return. [4] This technique is the most widely used practice for evaluating capital projects, being they acquisitions of companies or the purchases of machines. [5]
On the other hand, Net Present Value (NPV) is a valuation method used to evaluate investment projects. It relies on the estimated future cash flows of for the project discounting them to the present value, allowing a comparison with the initial investment. By accounting for startup costs and discounting future cash flows, NPV determines the net return on the investment. [1] [3] As it takes into consideration the time value of money and provides a concrete number (rates of return for the investment) that managers can use easily compare when making decisions. [6]
As can be assumed from the previous lines, the calculation of discounted cash flows for future years becomes critical for the investment decision, when it is based on the net present value of the considered project.
The article is starts explaining relevant concepts (Time Value of Money, Discount rates), continues with a description of the connection between Net Present Value and Discounted Cash Flows, followed by a presentation of the different ways of creating discounted cash flows. A brief example and a decision making rule is presented after introducing the Net Present Value concept, followed by application limitations. At the end, the article briefly highlights the key references used.
Big Idea
As stated in the abstract, the financial methods being considered in this report are strongly connected to each other. The NPV approach consists in discounting all future cash flows (both in- and out-flow) resulting from the project or investment opportunity under consideration with a given discount rate and then summing them together. [7]
A core principle for the mentioned methods is the Time Value of Money, a concept that expresses how money is worth more today than tomorrow. The second relevant concept is the discount rate used to determine the present value of future cash flows in NPV calculation. The choice of the discount rate can dramatically change the NPV analysis. Since it is an inverse function of the discount rate, the later has to be carefully selected. [8] It requires careful consideration of various factors, including the risk profile of the investment, the company's cost of capital and the expected return on alternative investments.
Time Value of Money
$1 of today is worth more than $1 of tomorrow
Time value of money (TVM) is a core financial principle that states a sum of money is worth more now than it will be in the future. [1]. This is because when the investor has the money available, it can be re-inverted generating more profits. Money available at different points in time has different values, which means that a sum of money’s value depends on how long you must wait to use it. The sooner you can use it, the more valuable it is. [9]
TVM plays a crucial role in investment analysis, particularly when assessing future cash flows and expected investment returns. Investors rely on this concept to assess businesses’ present values based on projected future returns, which helps them decide which investment opportunities to prioritize and pursue. [9] When investment options vary in time horizons, the TVM helps in determining the most profitable choice based on the present and future value of the money invested.
Discount Rate
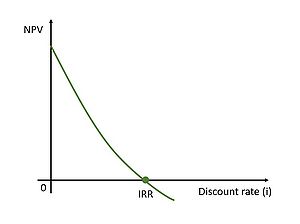
In corporate finance, a Discount Rate is the rate of return used to discount future cash flows back to their present value. It takes into consideration the time value of money and the risk associated with an investment. In other words, the discount rate is the interest rate used to convert future cash flows into their equivalent value in today’s dollars.[10]
When selecting a discount rate for an investment project, it's crucial to remember that the Net Present Value (NPV) is an inverse function of the rate. In other words, as the interest rate increases, the NPV decreases. This highlights the importance of selecting the appropriate discount rate, as it can significantly impact the calculated NPV for the project. [8] As observed in the image, the discount rate that gives a zero NPV is defined as the Internal Rate of Return (IRR). The IRR is a profitability measure that depends solely on the amount and timing of the project cash flows. [1]
When making project, program or portfolio management decisions, this rate value is often defined as the minimum acceptable rate of return that investors deem acceptable on an investment. The discount rate is determined by assessing the cost of capital, risks involved, opportunities in business expansion, rates of return for similar investments or projects, and other factors that could directly affect an investment or project under consideration. [11]
Here, two of the most widely used methods for defining the discount rate are presented:
- Cost of Capital: is the minimum required rate of return that an investor expects to earn on an investment to compensate the risk associated to it. The cost of capital is often used as a discount rate for evaluating investments that are similar in risk to the overall operations of the company. [12]
- Weighted Average Cost of Capital (WACC): WACC is a specific type of cost of capital where the cost of each type of capital is weighted by its percentage of total capital and they are added together. WACC is often used as a discount rate for projects or investments that are expected to have a similar risk profile as the overall operations of the company. [13]
As a general rule it can be said that Cost of Capital can be used as a discount rate when analyzing a particular investment. Whereas, the WACC is considered as a discount rate when considering a project as part of the portfolio of a company. [1] [14]
Discounted Cash Flow (DCF)
Discounted Cash Flow (DCF) is a valuation method that helps to estimate what an asset is worth today by using expected future cash flows. It uses future free cash flows projections (FCF) discounting them to get a present value that can be used to estimate the potential for an investment. The discount rate used when discounting the cash flows, reflects the risk associated with their estimation. [2] A DCF analysis reports how much money can be spent on the investment in the present in order to get a desired return in the future. This method operates under the time value of money principle and can be used to determine if in an investment or project is worthwhile comparing it to other alternatives. The mentioned analysis can be applied to value a stock, company, project, and many other assets or activities, and thus is widely used in both the investment industry and corporate finance management. [2]
The basic model valuation is given by:
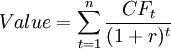
Where 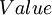 refers to the value of the asset;
refers to the value of the asset; 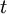 is the time period and ranged from 1 to n;
is the time period and ranged from 1 to n; 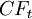 is the cash flow in period t; and
is the cash flow in period t; and 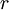 represents the discount rate. According to the model, the value of any asset is the present value of its expected cash flows. [2]
represents the discount rate. According to the model, the value of any asset is the present value of its expected cash flows. [2]
DCF valuation models
As stated earlier in this article, the projected cash flows of a firm or project become highly relevant for the NPV analysis. According to this, three basic DCF models can be identified and are: Dividend Discount Model (DDM); Free Cash Flow to Equity (FCFE); and Free Cash Flow to Firm (FCFF).
The first one is based on dividends, company's or project earnings that is distributed to its shareholders. Depending on company's policies, can be paid quarterly or yearly. [2] . Regarding the last two methods, they rely on Free Cash Flows calculations for equity investors (FCFE) or for the firm (FCFF). Free Cash Calculations refers to the cash flow a firm generates after taking into account non-cash expenses, changes in operating assets and liabilities, and capital expenditures. [15]
Dividend Discount Model (DDM)
Dividends it the most straightforward measure of cash flow as it goes directly to the equity investor.[2] In this model, the cost of equity is used as the discount rate for discounting estimated future dividends. It is assumed that the value of a firm's equity is the present value of the forecasted future dividends. [2]
Dividend Discount Model (DDM) prices a stock for a company by the sum of its future cash flows discounting them by the cost of equity. The value obtained with this model is used as the intrinsic value of the stock. [2]
The model uses a the formula previously presented where the dividends 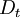 are calculated for each future period and discounted using the cost of equity as the discount rate
are calculated for each future period and discounted using the cost of equity as the discount rate 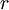 .
.
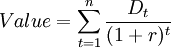
The presented version assumes that the stock is never sold and held for perpetuity. If the stock is held for a certain time period and sold at the end, the model can be adapted including the sale price of the stock. In this case, if the stock pays no dividends then the expected future cash flow is the sales price of it 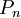 . [2]
. [2]
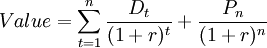
The main disadvantage of this method is that it can not be used to value stocks which do not pay any dividends.[2]
Free Cash Flow to Equity investors (FCFE)
FCFE investors is the cash flow remaining for returning cash through dividends or share repurchases to current common equity investors or for reinvesting in the firm after all obligations are satisfied. These obligations include debt payments, capital expenditures, changes in net working capital, and preferred dividend payments. For each year in the considered period for the investment, FCFE can be defined as follows: [15]
- FCFE = Net Income + Depreciation and Amortization - NonCash Working Capital - Gross Capital Expenditures + New Debt Issued - Debt Repayments [2]
Net Income is firm's earning after expenses and includes interest expenses and taxes. Depreciation and Amortization is a noncash adjustment added back to the income used to estimate the value of the business over the time. The Noncash Working Capital is obtained as the difference between noncash assets and current liabilities. [2] The balance between these three terms, define the cash flow from operating activities of a company. [15] The Gross Capital Expenditures is the cash flow generated from investing activities to acquire, upgrade, and maintain physical assets such as property, plants, buildings, technology, or equipment. [15] The difference between Net Debt Issued and Debt Repayments indicates the cash flow obtained from financing activities. [15]
When using the cash flows generated by this approach in a Net Present Value (NPV) analysis, then the appropriate discount rate to use for shareholders is the cost of equity. This rate represents the return that shareholders require for investing in the company and should be used to calculate the present value of future cash flows. [15] [2]
Free Cash Flow to the Firm (FCFF)
FCFF represents the cash available to fulfil the demand of capital to the firm coming from stockholders, bondholders and shareholders. [2] Consequently, FCFF is calculated before the sources of financing are determined and, as such, is not affected by the firm's financial structure. For each year in the considered period for the investment, FCFE can be defined as follows:[15]
- FCFF = EBIT * (1 - Tax Rate) + Depreciation and Amortization - Net Working Capital - Gross Capital Expenditures [2]
EBIT stands for Earnings Before Interest and Taxes and is multiplied by the remaining rate after considering taxes. FCFF includes, as before, the Depreciation and Amortization as non cash adjustments to the income together with the Net Working Capital. These three terms define the cash flow from operating activities. The Gross Capital Expenditures is the same as before, indicating the cash flow generated from investment activities. [15]
When using the cash flows generated by this approach in a Net Present Value (NPV) analysis, then the appropriate discount rate to use for investors is the Weighted Average Cost of Capital (WACC) to obtain the estimated company value. The obtained rate reflects the market value of the entire business since it represents the sum of investor claims on the firm’s cash flows from all those holding securities, including those holding long-term debt, preferred stock, common shareholders, and noncontrolling shareholders. Because it reflects all claims, the FCFF is a much more accurate estimate of a firm’s takeover value than simply a firm’s market value or equity capitalization. [15] [2]
Net Present Value (NPV)
The Net Present Value can be defined as the present value of the investment. It compares future net cash flows discounted to its present value, with the initial investment of the project.[5] The result obtained, represents the increase in the wealth of the investor along the time. As previously mentioned, the NPV analysis accounts for the time value of the money and can be used to compare different investment projects being under consideration. [16] The discount rate used to discount the cash flows is defined for each project under analysis and is associated with the investment risk profile. Riskier projects are discounted heavily. [7]
In corporate finance, the Net Present Value analysis is one of the tools that investors use when comparing investment projects and deciding which one to pursue. This method provides a concrete number that managers can use to easily compare an initial outlay of cash against the present value of the return. [6]
NPV combines projections of all net cash flows to assess the overall value of a project from the present view. Therefore the NPV is given by [7]:
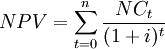
The difference between the cash inflows and cash outflows, gives the net cash flow, 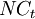 of the corresponding period. To obtain the present value of the project's life cycle, the net cash flows are summed over. If at the end of project's life cycle there is a liquidation value for the investment,
of the corresponding period. To obtain the present value of the project's life cycle, the net cash flows are summed over. If at the end of project's life cycle there is a liquidation value for the investment, 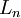 , it is also considered in the NPV calculation. The initial investment,
, it is also considered in the NPV calculation. The initial investment, 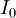 , is included in the calculation subtracting it from the overall sum of discounted net cash flows and the liquidation value. The NPV can be calculated as follows [7]:
, is included in the calculation subtracting it from the overall sum of discounted net cash flows and the liquidation value. The NPV can be calculated as follows [7]:
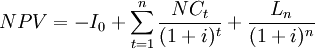
To clarify, when calculating the Net Present Value of a considered investment, the following steps are recommended to follow:[7]
- Identify the initial investment
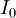 .
.
- Estimate the expected net cash flows,
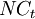 , for each period.
, for each period.
- Select the adequate discount rate,
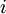 .
.
- Discount the calculated net cash flows to their present value following the given formula and obtain the summation. If the investment considers a liquidation value, discount it add it to the sum in the last period.
- Subtracting the initial investment,
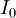 from the summation of present values, the Net Present Value (NPV) is obtained.
from the summation of present values, the Net Present Value (NPV) is obtained.
Example:
A company is considering two potential investment projects and wants to use NPV analysis to define the attractiveness of each project. As the company is comparing them with other investment alternatives with similar risk level, the discount rate to use is the weighted average cost of capital (WACC), assumed as 7%. Lets also assume that each project last five years, with the given initial investments and yearly cash flows and that the liquidation value is not considered:
| Initial investment | Cash Flow Year 1 | Cash Flow Year 2 | Cash Flow Year 3 | Cash Flow Year 4 | Cash Flow Year 5 | |
|---|---|---|---|---|---|---|
| Project A | $150,000 | $30,000 | $30,000 | $50,000 | $50,000 | $50,000 |
| Project B | $230,000 | $20,000 | $40,000 | $60,000 | $80,000 | $100,000 |
NPV for each project can be calculated using the formula as follows.
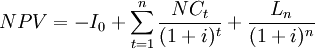
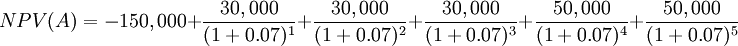
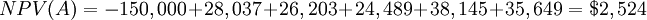
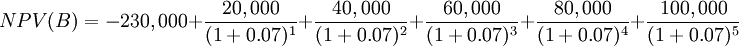
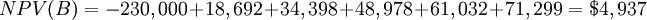
From the obtained results, it can be seen that both projects have a positive NPV being the NPV for Project B ($4,937) higher that the one for Project A ($2,524). In order to make a final decision, the NPV decision rule is considered.
NPV decision rule
The outcome of this method can be either positive or negative. A positive outcome could signify a worthwhile investment, resulting in a profitable return, whereas a negative value would indicate that the project’s return is not enough to make it profitable. A decisión rule is defined for the outcome obtained from the calculation of the NPV.[8]
| Condition | Meaning | Decision |
|---|---|---|
| If NPV>0, | The benefits deriving from the investment opportunity exceed the costs in the amount of the NPV. | The investment deserves to be made. |
| If NPV<0, | The discounted cash flows doesn’t cover the initial investment generating a decreased profit in an amount equal to the negative NPV. | The investment should be rejected. |
| If NPV=0, | It means that the sum of the cash flows discounted to their present value are equal to the amount of the initial investment. | The opportunity doesn’t generate profits or losses and other decision criteria should be implemented. |
Besides the mentioned decision rule, a profitability criteria can also be implemented when considering one or more projects (as in the example).
- For single project analysis, the decision is based on the NPV decision rule. Accept projects with positive NPV (NPV>0).
- When comparing several projects, the one with the highest NPV should be the one selected.
In the example, both projects have a positive NPV so both can potentially be accepted. But as Project B returned a higher value than Project A, then B should be the one accepted.
Limitations when using DCF and NPV
- DCF method is considered forward looking as it depends on future expectations rather than historical results. It implies that require considerable assumptions regarding cash flows input and output estimations, the discount rate to use and a potential terminal value. [2] Every project in unique and has its own distinct set of processes, which can make it difficult to accurately estimate cash flows. [14] This means there's a greater chance of mistakes being made.
- When using the NPV method to make investment decisions, the chosen discount rate plays a crucial role. [8] If the rate is set too low, suboptimal investments may be selected, whereas a rate that's too high could lead to good investments being rejected. Additionally, the NPV calculation assumes that the discount rate will remain constant over the duration of the project. This can be solved including variable discount rates.[3]
- The terminal value represents a large percentage of total DCF valuation. Hence, valuation predominantly depends on the terminal assumptions rather than operating assumptions for the DCF. [2] Since slightly changes in the terminal value could result in large fluctuations in the analysis, the data collection and estimations should be accurate. [3]
- The NPV analysis is expressed in absolute values, not in relative terms, meaning that only projects with the same length can be compared. This is because larger projects could potentially generate higher returns. [1]
Bibliography
Brealey, R., Myers, S., Allen, F., Principles of Corporate Finance, 10th edition, McGraw-Hill Irwin, 2010
Chapter 5 in this book presents the Net Present Value as investment evaluation criteria and compares is with other financial metrics, such as payback period and book rate of return. It also highlights the need for more accurate methods when making substantial capital investment decisions. It presents the expected rate of return rule as an alternative to calculating NPV, and discusses its advantages and potential pitfalls.
Žižlavský O., Net present value approach: method for economic assessment of innovation projects., 19th International Scientific Conference, Economics and Management, (2014), pp. 506-512
The research paper provides a comprehensive understanding of the NPV method for project appraisal. It emphasizes the importance of the time value of money and selecting an appropriate discount rate. This paper serves as a valuable resource for anyone seeking to gain insights into the NPV approach.
Ferrari, C., Bottasso, A., Conti, M. and Tei, A., Ch. 5 - Investment Appraisal. In: Economic role of transport infrastructure: Theory and models (2018), pp. 85-114
Chapter 5 covers financial appraisal methods, highlighting the importance of net present value (NPV) and its relationship with discount rates. It stresses the need to select appropriate discount rates when appraising projects using NPV and introduces sensitivity analysis as a crucial tool for accurate financial evaluations. Overall, the chapter provides readers with the necessary knowledge to make informed financial decisions and maximize profitability.
Kumar R., Ch 6 - Discounted cash flow valuation models. In: Valuation (2016),pp. 145-185
Chapter 6 presents a detailed explanation about three DCF valuation models: Dividend Discount (DDM), Free Cash Flow to Equity (FCFE), and Free Cash Flow to Firm (FCFF). It also applies the methods considering valuation models with nonconstant growth in two and three different stages. Overall, the chapter provides a technical explanation about the applicability of the valuation models and its financial impact for the investor point of view.
DePamphilis, D., Ch 7 - Mergers and Acquisitions Cash Flow Valuation Basics., In: Mergers, Acquisitions, and Other Restructuring Activities (2018, 9th Edition),pp. 235-276
Chapter 7 provides a brief review of fundamental finance concepts, such as risk and return, and introduces the concepts of free cash flow to equity and to the firm for use in valuation. The chapter concludes with a practical illustration of the enterprise method for estimating a firm's equity value. These concepts and techniques are essential for anyone studying or working in finance and corporate valuation.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Brealey, R., Myers, S., Allen, F., Principles of Corporate Finance, 10th edition, McGraw-Hill Irwin, 2010 https://zlib.pub/book/principles-of-corporate-finance-8qquurke17u0
- ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 Kumar R., Ch 6 - Discounted cash flow valuation models. In: Valuation (2016),pp. 145-185, https://doi.org/10.1016/B978-0-12-802303-7.00006-1
- ↑ 3.0 3.1 3.2 3.3 Ungki L., Choice data generation using usage scenarios and discounted cash flow analysis., Journal of Choice Modelling, (2020), https://doi.org/10.1016/j.jocm.2020.100250
- ↑ Corporate Finance Institute: Discounted Cash Flow "https://corporatefinanceinstitute.com/resources/valuation/discounted-cash-flow-dcf/"
- ↑ 5.0 5.1 Benninga, S., Financial Modeling, 4th edition, The MIT Press, 2014 https://zlibrary.to/pdfs/financial-modeling
- ↑ 6.0 6.1 Harvard Business Review: A Refresher on Net Present Value "https://hbr.org/2014/11/a-refresher-on-net-present-value"
- ↑ 7.0 7.1 7.2 7.3 7.4 Žižlavský O., Net present value approach: method for economic assessment of innovation projects., 19th International Scientific Conference, Economics and Management, (2014), pp. 506-512 https://doi.org/10.1016/j.sbspro.2014.11.230
- ↑ 8.0 8.1 8.2 8.3 8.4 Ferrari, C., Bottasso, A., Conti, M. and Tei, A., Ch. 5 - Investment Appraisal. In: Economic role of transport infrastructure: Theory and models (2018), pp. 85-114 https://doi.org/10.1016/C2016-0-03558-1
- ↑ 9.0 9.1 Harvard Business School: Time Value of Money "https://online.hbs.edu/blog/post/time-value-of-money"
- ↑ Corporate Finance Institute: Discount Rate "https://corporatefinanceinstitute.com/resources/valuation/discount-rate/"
- ↑ Corporate Finance Institute: Hurdle Rate "https://corporatefinanceinstitute.com/resources/valuation/hurdle-rate-definition/"
- ↑ Harvard Business Review: Cost of Capital "https://hbr.org/2015/04/a-refresher-on-cost-of-capital"
- ↑ Corporate Finance Institute: Weighted Average Cost of Capital "https://corporatefinanceinstitute.com/resources/valuation/what-is-wacc-formula/"
- ↑ 14.0 14.1 International Organization for Standardization (ISO), Project, program and portfolio management – Guidance on Project Management (DS/ISO 21502:2020), 2021 Edition.
- ↑ 15.0 15.1 15.2 15.3 15.4 15.5 15.6 15.7 15.8 DePamphilis, D., Ch 7 - Mergers and Acquisitions Cash Flow Valuation Basics. In Mergers, Acquisitions, and Other Restructuring Activities (2018, 9th Edition), pp. 235-276, https://doi.org/10.1016/B978-0-12-801609-1.00007-5
- ↑ Corporate Finance Institute: Net Present Value "https://corporatefinanceinstitute.com/resources/valuation/net-present-value-npv/