Resource Leveling in Construction Projects
Abstract
Management of the resources carries an indispensable importance for profitability and scheduling of construction projects. Construction projects require different sets of skills, equipment and materials at different stages. Furthermore, the demand for amount of distinct assets fluctuates greatly depending to the project stage. Resource Leveling, also known as Resource Smoothing, shows interest in eliminating resource shortages and abundances by having a more optimized project schedule with regards to the utilization of the resources. The goal of the Resource Leveling is eliminating delays, failures and cost overruns, without interfering with the project’s scope, cost and time constraints. In Resource Leveling, the project duration, number of the resources and the completion date remains unchanged. It is assumed that the project has been provided sufficiently. Resource Leveling is closely tied to the project scheduling methods such as Critical Path Method (CPM) and Program Evaluation and Review Technique (PERT), which are predominantly used in construction industry. Usually, Resource Leveling is coupled with one them. Whereas, these scheduling techniques are interested in critical tasks and their connections to each other for completion of the project, they fail foreseeing any failures due to shortcomings. Resource Leveling takes advantage of float and moves tasks around in timetable with an eye on resources. Coming up with more efficient solutions for more balanced use is an area that has been attracting interest. For this purpose, various methods, algorithms and objective functions have been developed. The users have opportunity to select between them according to their project in order to achieve best results. They are explained and an example is given.
Contents |
Introduction
Construction projects are complex and costly ventures with uneven work load through the timeline. For success of a project in construction sector, multiple stakeholders should be satisfied, multiple requirements should be met by the management. Time, cost and quality are most commonly used and linked evaluation criteria for the success of a construction project [4]. Despite the efforts of projects managers, construction projects often fail to be completed on time [4]. Delivering on time is strictly tied to the resource management. Inadequate management of the resources may cause severe delays and cost overruns because of resource shortages and abundances in different cases [3]. Resource leveling is a method in order to eliminate delays because of uneven resource consumption and availability. Resource leveling assumes that there are sufficient resources, but the project duration is constant. The main idea behind resource leveling is moving non critical activities in the schedule for eliminating fluctuations, peaks and valleys in resource utilization [3]. It is impossible to have a completely flat resource consumption, hence, it is important to identify appropriate objective function for achieving a resource use as uniform as possible or having a non-uniform distribution which is in accordance with the project’s needs. Computing abilities are important. Depending on the limitations, needs and processing power, an optimization method can be implemented. All methods have their own advantages and disadvantages, thus each of them suits different problems.
Overview
Construction projects consist of multiple independent and linked tasks. Interlinked task structure creates scheduling problems which are solved by using scheduling tools such as PERT and CPM. These particular scheduling techniques demonstrate a network of tasks. On the other hand, each of the tasks require availability of different kind and different amount of resources for completion. As a result, resource consumption of construction projects varies according to the schedules. Scheduling tools focus on project duration rather than resource use. The main purpose of resource leveling is to minimize waving in resource consumption without changing the delivery date and total resource use [1]. Resource leveling shifts start and completion dates of suitable tasks. Production interruptions may cause delays and extra costs. Therefore, resources should be managed efficiently for preventing project failures [2].
Resource leveling benefits from schedule flexibility. In a construction project, there are multiple independent tasks which can be realized simultaneously and there are some other tasks which demand completion of certain prior tasks. It is possible to rearrange dates of certain independent tasks in the available time without postponing start date of a later task. This time availability is called float. Resource leveling moves the tasks in their available float with the purpose of reducing fluctuations in resource consumption. In reality, the resources are limited and concurrently demanded by several activities, which results in shortages and abundances [2].
There are nine popular objective functions in resource leveling. Each objective function optimizes different parameters. They suit for different problems. The scheduler identifies a goal in resource leveling by deciding on one of them according to the project’s needs. The scheduler uses one of the Approach Methods for optimization. In chronological order, they are Exact Method, Heuristic Method and Metaheuristic Method. It's also possible to solve manually. All methods have their strengths and weaknesses over each other. They differ in suitability to different project complexity levels and time requirements for computation.
Scheduling Techniques and Resource Leveling
Resource leveling isn’t a technique that can be implemented to construction projects solely. Resource leveling is often coupled with a scheduling method, because resource leveling requires knowledge on the schedule of the project for rearranging start dates of non-critical activities (activities that doesn’t cause any delay when the schedule is changed). Construction projects use several scheduling techniques, namely Gantt Charts, Critical Path Method (CPM) and Program Evaluation and Review technique (PERT) [2]. However, each of these scheduling techniques have some shortcomings. The Gantt Chart simply demonstrates the durations of the activities but it doesn’t display a network. The Gantt Chart cannot determine connections between individual activities; hence Gantt Chart cannot be used for defining debut and completion times of the activities [1]. Even though they have drawbacks, CPM and PERT, which are network-based scheduling techniques, have been commonly used in construction projects [1]. Critical Path Method has been the most popular scheduling technique since the 1950s [1]. A complete network of activities demonstrates the links between the activities and their durations [1]. The Critical Path Method has the disadvantage of assuming that all the resources are unlimited [2]. Although network based scheduling techniques are the pillars in scheduling in construction projects, they don’t pay attention to the resource availability and they focus on minimizing the construction duration [1]. This prioritization can easily cause peaks and valleys in resource utilization.
Schedule Flexibility and Float
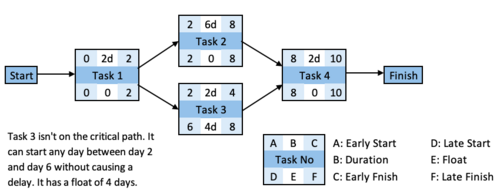
Construction projects consist of multiple distinct and complex tasks. Some tasks are independent but tasks depend on certain prior tasks. Dependent tasks require completion of certain prior tasks before start because they are structured as the next links in the chain. Many independent tasks can be completed simultaneously if enough resources are present. Every task have distinct time and resource requirements and task may become a node in the project schedule. Even though, some of these tasks can be completed in shorter durations, the project team has to wait for completion of all required prior tasks. In other words, the longest task or task set determine the start date of the later tasks in the same work chain.
Resource leveling alters the schedule of the construction project. It is possible to rearrange the dates of some independent tasks or some necessary tasks which demands less time than other crucial tasks without changing the total duration of the work chain. The total availability of float gives schedule flexibility [5]. The scheduler should find a balance between resource use and schedule flexibility while producing a solution for resource leveling problem [1]. The time availability, which allows move of the start and completion dates of certain tasks without changing total duration, is called float. If a task is suitable for resource leveling, the start time of the task moves forward or backward by using total float [3]. Float is a valuable commodity for both clients and contractors in construction sector [1]. On the other hand, inconsiderate consumption of the float is dangerous. Because, in that case, activities become critical. Any unexpected delays or problems in activities which doesn’t have float would cause delays and potentially cost overruns [5]. An amount of float can be left while rescheduling non critical activities as a precaution. Schedule flexibility is essential for resource leveling and it can also be a safety factor.
Objective Functions
An objective function must be selected for resource leveling. Objective functions designate the parameter which will be minimized in order to receive the best outcome for the project’s needs. They define the target of the resource leveling process. A literature review on resource leveling shows that there are nine common objective functions and each of them optimizes differently [2]. To put it another way, nine objective functions return nine different solutions because they aim to minimize different parameters [2]. Objective functions and formulas are given below :
1. Minimization of the sum of the absolute deviations in daily resource usage [2]
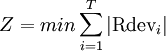
min = minimize
i = day under consideration
T = the duration of the project
Rdevi = deviation between resources required on day i and i+1
2. Minimization of the sum of only the increases in daily resource usage from one day to the next [2]
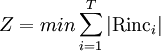
min = minimize
i = day under consideration
T = the duration of the project
Rinci = increase in between resources required on day i and i+1
3. Minimization of the sum of the absolute deviations between daily resource usage and the average resource usage [2]
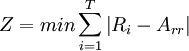
min = minimize
i = day under consideration
T = the duration of the project
Ri = resources required on day i and i+1
Arr = average resource usage
4.Minimization of the maximum daily resource usage [2]
![Z=min\left[max\left(R_i\right)\right]](/images/math/9/2/e/92edb4d60f2cc050442d144b507e9099.png)
min = minimize
max = maximum
i = day under consideration
Ri = resources required on day i and i+1
5. Minimization of the maximum deviation in daily resource usage [2]
![Z=min\left[max\left|{\rm Rdev}_i\right|\right]](/images/math/2/2/d/22daa22c15cc590ba45fa5e0090da2f0.png)
min = minimize
max = maximum
i = day under consideration
Rdevi = deviation between resources required on day i and i+1
6. Minimization of the maximum absolute deviation between daily resource usage and the average resource usage [2]
![Z=min\left[max\left|R_i-A_{rr}\right|\right]](/images/math/5/6/b/56b26ed26f4c267e930c7e9625f0257e.png)
min = minimize
max = maximum
i = day under consideration
Ri = resources required on day i and i+1
Arr = average resource usage
7. Minimization of the sum of the square of daily resource usage [2]
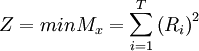
min = minimize
i = day under consideration
T = the duration of the project
Ri = resources required on day i and i+1
8. Minimization of the sum of the square of the deviations in daily resource usage [2]
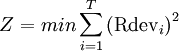
min = minimize
i = day under consideration
T = the duration of the project
Rdevi = deviation between resources required on day i and i+1
9. Minimization of the sum of the square of the deviations between daily resource usage and the average resource usage [2]
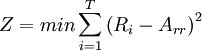
min = minimize
i = day under consideration
T = the duration of the project
Ri = resources required on day i and i+1
Arr = average resource usage
Optimization Methods
After determining objective functions, optimization starts. The schedule can be optimized manually or a method can be used. Optimization method determines the pathway which will be taken in order to reach to the desired optimization result. Numerous models have been produced through the years. Three main groups can be identified, namely: exact algorithms, heuristic methods and metaheuristics [2]. It is also possible to combine them and have a hybrid approach. All methods have their own strengths and weaknesses; hence they are suitable for different situations. Their distinctions are mostly in the accuracy of the solution, computation load and speed. Because of the differences, different optimization methods are suitable for problems at different complexity levels.
1. Exact Method
Exact method is known with several other names such as exact algorithms or mathematical method. It also provides a base for other optimization methods. In exact method, the solution is searched by applying multiple steps. It is a repetitive process with finite number of iterations (linear programming, branch and bound algorithms). The algorithms can be beneficial for simpler and smaller problems but they may fail to deliver results for complex optimization problems. Exact algorithms aren’t suitable for large scale problems because they are inefficient due to consumption of greater amounts of processing power and time for optimal solution [2].
2. Heuristic Method
Heuristic method simplifies and eliminates some aspects of the exact method with the user’s experience and point of view. The options are narrowed. Rule of thumb is an example to heuristic approach. Heuristic method can provide substantially faster calculations in comparison to the exact method. As a result of the speed gain, heuristic approach can be a more convenient method for large scale problems. But heuristic method doesn’t guarantee an optimal solution, it may still fail to deliver solution for complex optimization problems [2].
3. Metaheuristic Method
Metaheuristic method takes inspiration from the nature and tries to replicate natural phenomenons in calculations. The reasoning behind this method is the thought that everything in the nature is in its most efficient form for survival. The approach is generating a solution in a short time by mimicking effectiveness of the nature. Metaheuristics can serve for providing solutions to complex optimization problems [2]. Metaheuristic method mainly focuses on iterative process for near optimal results. Metaheuristics link heuristic approach with different learning strategies for structuring information and iteratively searching in a larger space in order to efficiently produce near optimal solutions [2]. Two commonly used metaheuristic approaches by researchers are genetic algorithm, which takes inspiration from biological evolution, and particle swarm optimization [4]. The metaheuristic method is fast but it may fail to generate the best results in all conditions.
Example with CPM
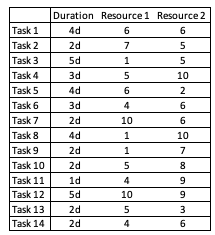
A construction company gets hired as a subcontractor in a construction project. The company should deliver 14 tasks in 24 workdays. Tasks are only dependent in each other. Other contractor’s work doesn’t have effects on the 14 tasks. Every task uses two independent resources, namely Resource 1 and Resource 2. Resource consumption is measured with numbers from 1 to 10. It is assumed that a task constantly consumes given number of resources every day till completion of the task. Durations of tasks, and their respective resource consumptions are given below.
For example: Task 1 consumes 6 units of “Resource 1” every day for 4 days.
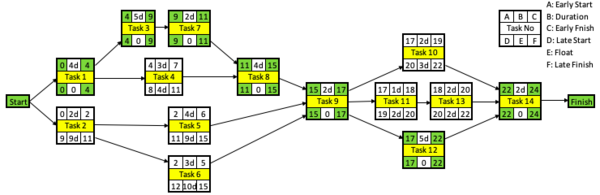
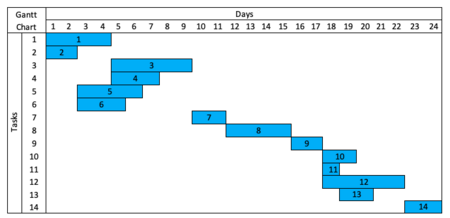
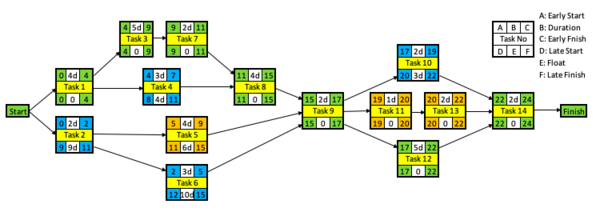
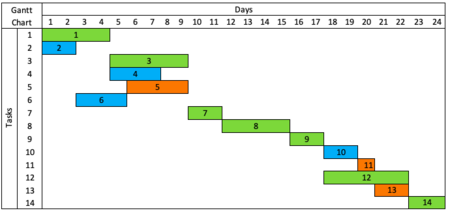
Critical Pathway Method is commonly used in construction projects, because it shows dependencies between tasks. CPM of 14 tasks is given below. The schedule follows early start and early finish dates without using available float. Green boxes are start and finish dates of the tasks on the critical path. In other words, tasks without float or tasks which can’t be rescheduled for resource scheduling. Their rescheduling would alter the project duration. Yellow boxes are task numbers. A Gantt Chart is below for better visualization.
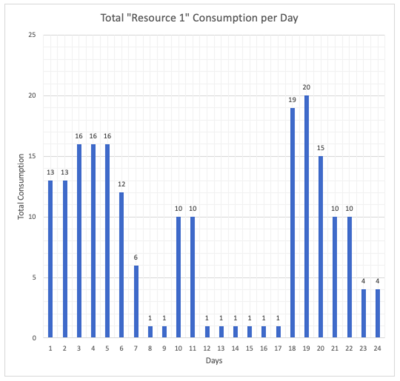
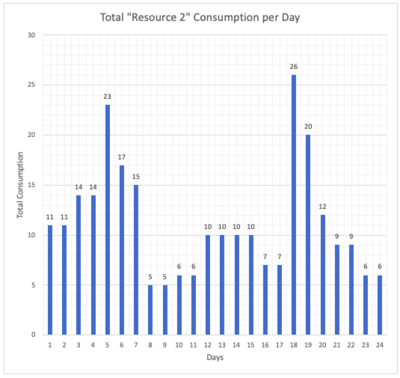
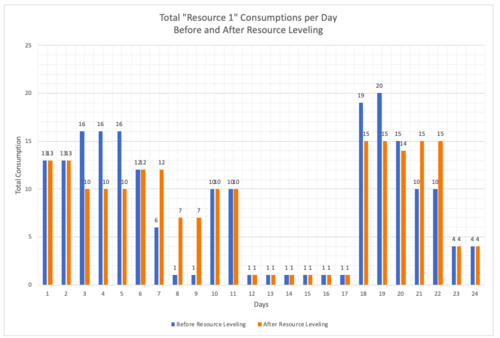
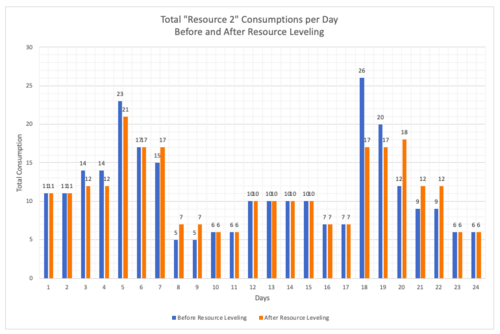
When the tasks are scheduled according to the CPM above, daily consumption of Resource 1 and Resource 2 are given below. Drastic rises, peaks and valleys can be observed on the graphs.
The data given above explains the situation before resource leveling. The aim of the resource leveling is having a more balanced resource consumption. First of all, an objective function should be selected. Objective function defines the parameter which will be optimized. Minimization of the sum of the absolute deviations between daily resource usage and the average resource usage [2] is the objective function for this example. Then, an optimization method should be selected. This example uses manual optimization. The new CPM and the new Gantt chart can be seen below. Orange represents rescheduled tasks and blue represents tasks which have available float but not rescheduled.
The tasks are rescheduled for having a more even resource consumption during 24 days of work. Task 11 and Task 13 consume all available floats. The graphs below show the change. Orange columns show new daily resource consumption and the blue columns show daily consumption before resource leveling.
From the graphs above, it can be seen that peaks are lowered and the changes in consumption are less drastic. The standard deviation for Resource 1 and Resource 2 consumption before leveling are 6,49 and 5,54 respectively, they are 5,24 and 4,40 after leveling.
Annotated Bibliography
1. Damci, Atilla, et al. "Use of float consumption rate in resource leveling of construction projects." Frontiers of Engineering Management (2022): 1-13.
The article investigates resource leveling for eliminating delays. The article introduces a float consumption rate which is the percentage of use of available float. It develops a model. In the model, the scheduler appoints consumption rates. The article gives information on resource leveling, float, schedule flexibility and scheduling techniques.
2. Damci, Atilla, and Gul Polat. "Impacts of different objective functions on resource leveling in construction projects: a case study." Journal of civil engineering and management 20.4 (2014): 537-547.
The article investigates nine different objective functions; their effectiveness and differences on resource leveling. It also gives information on optimization methods. The article finds improvement percentages. The article explains calculations in resource leveling.
3. Damci, Atilla, et al. "Resource levelling with float consumption rate." Creative Construction Conference 2019. Budapest University of Technology and Economics, 2019.
The conference paper proposes a model with consumption rates. It introduces a case study and demonstrates the visual basic based model. It gives information on importance, theory and practice of resource leveling.
4. Akin, Firat Dogu, et al. "A crashing-based time-cost trade-off model considering quality cost and contract clauses." International Journal of Construction Management (2021): 1-10.
The article focuses on time and cost swap in construction projects and investigates crashing. It develops a crashing model and compares it with two metaheuristic optimization methods. The article gives information on success criteria of the projects and metaheuristic approach.
5. Turkoglu, H., Polat, G., & Akin, F. D. (2023). Crashing construction projects considering schedule flexibility: an illustrative example. International Journal of Construction Management, 23(4), 619-628.
The article investigates using crashing with scheduling strategies in construction projects. The article gives information on schedule flexibility and works with float. It proposes a model to increase schedule flexibility. It tests the work with Monte Carlo simulation.
References
1. Damci, Atilla, et al. "Use of float consumption rate in resource leveling of construction projects." Frontiers of Engineering Management (2022): 1-13.
2. Damci, Atilla, and Gul Polat. "Impacts of different objective functions on resource leveling in construction projects: a case study." Journal of civil engineering and management 20.4 (2014): 537-547.
3. Damci, Atilla, et al. "Resource levelling with float consumption rate." Creative Construction Conference 2019. Budapest University of Technology and Economics, 2019.
4. Akin, Firat Dogu, et al. "A crashing-based time-cost trade-off model considering quality cost and contract clauses." International Journal of Construction Management (2021): 1-10.
5. Turkoglu, H., Polat, G., & Akin, F. D. (2023). Crashing construction projects considering schedule flexibility: an illustrative example. International Journal of Construction Management, 23(4), 619-628.