Resource-Constrained Critical Path Method
(→Step 1) |
(→Step 1) |
||
| Line 46: | Line 46: | ||
===Step 1=== | ===Step 1=== | ||
| − | + | [[File:Network Diagram.jpg|thumb|400px|Activity list and network diagram]] | |
| − | [[File:Network | + | |
| − | + | ||
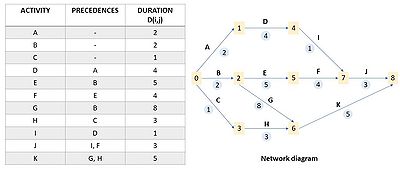
The first step in CPM is constructing an arrow diagram that can show the precedence relationships among the project tasks. | The first step in CPM is constructing an arrow diagram that can show the precedence relationships among the project tasks. | ||
Generally, it starts by making a list of all the activities to be performed in the project, a list of the precedences and the relative duration. Based on this information, the network diagram can be constructed. Here, each arrow (capital letter) represents an activity; arrowheads show the order of each task. A node (number) indicates the beginning and the end of the activity; circled numbers stand for the duration of the activities. | Generally, it starts by making a list of all the activities to be performed in the project, a list of the precedences and the relative duration. Based on this information, the network diagram can be constructed. Here, each arrow (capital letter) represents an activity; arrowheads show the order of each task. A node (number) indicates the beginning and the end of the activity; circled numbers stand for the duration of the activities. | ||
| − | + | [[File:dummy.jpg|thumb|400px|Dummy activity example]] | |
The construction basically follows four rules<ref name=FEES />: | The construction basically follows four rules<ref name=FEES />: | ||
#Each activity is represented by one arrow in the network; | #Each activity is represented by one arrow in the network; | ||
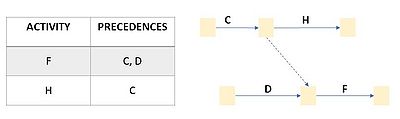
| − | #"Dummy" activities (dotted arrows) are created whenever needed to portray the logic of the relationship between activities. A dummy activity represents an activity which takes no time and uses no resources; | + | #"Dummy" activities (dotted arrows) are created whenever needed to portray the logic of the relationship between activities. A dummy activity represents an activity which takes no time and uses no resources; |
#Two activities shouldn't be identified by the same beginning event and by the same end event. | #Two activities shouldn't be identified by the same beginning event and by the same end event. | ||
#The following questions must be answered as each activity is added to the network, to ensure the network correctness: | #The following questions must be answered as each activity is added to the network, to ensure the network correctness: | ||
Revision as of 21:21, 21 February 2019
Developed by Giorgia Scartozzi
This article aims to describe a new approach to a specific project management technique called Critical Path Method (CPM).
According to Project Management Body of Knowledge (PMBOK), CPM is a method used to estimate the minimum project duration and determine the amount of scheduling flexibility on the logical network paths within the schedule model[1]. Given scheduled activities for a project that need to be completed in a specific order, multiple task sequences can be defined. CPM helps us to determine the longest sequence of tasks in the project, which will be also the shorter possible project duration. Thus, the main steps of CPM will be described, providing a brief guidance on how to apply the method so to obtain the optimal project duration.
However, a traditional CPM schedule is not realistic, because it assumes unlimited resources, some of which are highly limited in practice[2]. Therefore, a different approach of the same technique, called Resource-constrained Critical Path Method (RCPM), will be presented. By providing a step-by-step RCPM procedure, the article will focus on the advantages that this method can offer compared to the traditional Critical Path Method. The paper will then conclude with observations about the benefits and limitations of both CPM and RCPM, highlighting differences and similarities between the two techniques.
Contents |
Overview
What is Project Management?
The definition of 'project' can be found in the Project Management Body of Knowledge: it is a temporary endeavor undertaken to create a unique product, service, or result[1]. Ergo, a project is any series of activities and tasks having a specific objective to be completed within some specifications[3], such as start and end dates, specific goals and limits, established implementers responsibilities, budget and schedule[4].The management of a project is essential to ensure that these activities are completed in accordance with all the given specifications and expectations[5]. Therefore, 'project management' can be defined as the application of knowledge, skills, tools, and techniques to project activities to meet the project requirements[1]. It is the process of defining, planning, organizing and controlling tasks in order to deliver a project in time and at a reasonable cost.
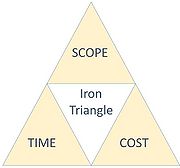
The project management success can be measured through the "iron triangle" model that includes time, scope, and cost. The success of a project should, therefore, be measured within project scope, scheduling, cost, quality, resource, and risk constraints in term of completing the project [6].
Scheduling is an important and difficult task during project planning since it helps to monitor the project duration and resource utilization. The challenge is about the scheduling complexity and dynamism: in fact, plans can change before the start but even during the implementation[4]. In order to better manage projects and face the changes that may occur over time, a lot of methods were created, and among them, the Critical Path Method (CPM) is one of the better-known planning and control techniques in project scheduling.
The Critical Path Method
Proposed for the first time in 1956 during a collaboration between Morgan R. Walker (DuPont) and James E. Kelley Jr (Remington Rand), the Critical Path Method is a deterministic technique developed with the purpose of planning, managing, organizing and analyzing the total time involved in a project. The method attempts to establish the trade-off between the overall cost of the project and the total time for the completion of desired activities[5].
To perform this technique, it is fundamental the use of a network diagram to show logical relationships between the activities of a project, usually represented by arrows (activities) and nodes (beginning and end of the activities). CPM identifies the critical and non-critical paths on this precedence-relationship network, enabling managers to be more focused on those critical activities that can assure the project completion by the deadline. Minimum project duration can be estimated by using this algorithm, that can also provide parameters of activities including earliest starting time (ES), latest starting time (LS), earliest finish time (EF), latest finish time (LF), maximum available time and slack time, or total float[3].
In this regard, we can define:
- Earliest starting time (ES): the earliest time at which the task can start, given that its precedent tasks must be completed first;
- Earliest finish time (EF): the earliest start time for the task plus the time required to complete the task;
- Latest finish time (LF): the latest time at which the task can be completed without delaying the project;
- Latest starting time (LS): the latest finish time minus the time required to complete the task.
Moreover, two important concepts need to be explained: the total float and the free float. According to the PMBOK, the total float is the amount of time that a schedule activity can be delayed or extended from its early start date without delaying the project finish date or violating a schedule constraint, whereas the free float is the amount of time that a schedule activity can be delayed without delaying the early start date of any successor or violating a schedule constraint[1]. The monitoring on these two floats is an important task for a project manager because they indicate the activities in the project that most constrain the schedule[7].
How to use the Critical Path Method
The Critical Path Method comprises several steps, but they can be summarized in four main phases:
- Drawing the network diagram to show the existing relationships between activities to be performed in the project;
- Estimating time involved in each activity;
- Actual scheduling, checking the dependencies among activities and taking into account both necessary resources and available resources;
- Monitoring.
Step 1
The first step in CPM is constructing an arrow diagram that can show the precedence relationships among the project tasks.
Generally, it starts by making a list of all the activities to be performed in the project, a list of the precedences and the relative duration. Based on this information, the network diagram can be constructed. Here, each arrow (capital letter) represents an activity; arrowheads show the order of each task. A node (number) indicates the beginning and the end of the activity; circled numbers stand for the duration of the activities.
The construction basically follows four rules[7]:
- Each activity is represented by one arrow in the network;
- "Dummy" activities (dotted arrows) are created whenever needed to portray the logic of the relationship between activities. A dummy activity represents an activity which takes no time and uses no resources;
- Two activities shouldn't be identified by the same beginning event and by the same end event.
- The following questions must be answered as each activity is added to the network, to ensure the network correctness:
- What activities must be completed immediately before this activity can start?
- What activities must follow this activity?
By applying these rules, the precedence-relationship diagram can be designed, and it will represent the master plan or working model of the entire project[8].
Step 2
The second step involves the calculation of the start and finish times for each activity. Using the duration shown in the previous list and the network that resulted from it, the earliest times and the latest times can be determined. The calculations of these times constitute, respectively, the forward pass and the backward pass.
In the forward pass, computation begins from the start node and continues until the end node. For event 1, it is assumed that the ETE is equal to 0. Supposing that for an event i ETE(i) is known, ETE(j) for the event j can be calculated with
- ETE(j) = max [ETE(i) + D(i, j)]
This calculation can be done for all the activities in the diagram. It is conventional to define the project time as the ETE of the end event; in this case, the project time is the minimum amount of time needed to finish the project[7].
The Resource-constrained Critical Path Method
Observations
References
- ↑ 1.0 1.1 1.2 1.3 Project Management Institute, "A guide to the project management body of knowledge (PMBOK® guide) - Fifth edition". (2013)
- ↑ Kyunghwan Kim and Jesùs M. de la Garza, "Phantom Float". Journal of Construction Engineering and Management, Volume 129, No. 5 (October 1, 2003)
- ↑ 3.0 3.1 Paing Hein Soe and Thein Min Htike, "Critical Path Analysis programming method without network diagram". MATEC Web Conference, Volume 192 (2018)
- ↑ 4.0 4.1 Rafik Nafkha and Artur Wilinski, "The Critical Path Method in estimating project duration". Information Systems in Management, Volume 5, No. 1, Pages 78−87 (2016)
- ↑ 5.0 5.1 Nishi Sharma and S. B. Gupta, "Applications of Critical Path Method in Project Management". International Journal of Management and Economics, Volume 1, No. 26 (November 2018)
- ↑ Arin Wulandari, M. Dachyar and Farizal, "Scheduling of Empennage Structure Design Project of Indonesia’s Aircraft with Critical Path Method (CPM)". MATEC Web Conferences, Volume 248 (2018)
- ↑ 7.0 7.1 7.2 Earl B. Anderson and R. Stanton Hales, "Critical Path Method Applied to Research Project Planning: Fire Economics Evaluation System (FEES)". Gen. Tech. Rep. PSW-GTR-93. Berkeley, CA: U.S. Department of Agriculture, Forest Service, Pacific Southwest Forest and Range Experiment Station. 12 p. (1986)
- ↑ R.L. Martino, "Applying Critical Path Method to System Design and Installation". Control Engineering, Volume 10, Issue 2, pp. 93-98 (1963)