Resource-Constrained Critical Path Method

Developed by Giorgia Scartozzi

This article aims to describe a new approach to a specific project management technique called Critical Path Method (CPM).

According to Project Management Body of Knowledge (PMBOK), CPM is a method used to estimate the minimum project duration and determine the amount of scheduling flexibility on the logical network paths within the schedule model. Given scheduled activities for a project that need to be completed in a specific order, multiple task sequences can be defined. CPM helps us to determine the longest sequence of tasks in the project, which will be also the shorter possible project duration. Thus, the main steps of CPM will be described, providing a brief guidance on how to apply the method so to obtain the optimal project duration.

However, a traditional CPM schedule is not realistic, because it assumes unlimited resources, some of which are highly limited in practice. Therefore, a different approach of the same technique, called Resource-constrained Critical Path Method (RCPM), will be presented. By providing a step-by-step RCPM procedure, the article will focus on the advantages that this method can offer compared to the traditional Critical Path Method. The paper will then conclude with observations about the benefits and limitations of both CPM and RCPM, highlighting differences and similarities between the two techniques.

Overview

What is Project Management?

The Iron Triangle - Scope, Time, Cost

The definition of 'project' can be found in the Project Management Body of Knowledge: it is a temporary endeavor undertaken to create a unique product, service, or result. Ergo, a project is any series of activities and tasks having a specific objective to be completed within some specifications, such as start and end dates, specific goals and limits, established implementers responsibilities, budget and schedule.

The management of a project is essential to ensure that these activities are completed in accordance with all the given specifications and expectations. Therefore, 'project management' can be defined as the application of knowledge, skills, tools, and techniques to project activities to meet the project requirements. It is the process of defining, planning, organizing and controlling tasks in order to deliver a project in time and at a reasonable cost.

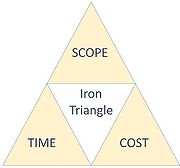
The project management success can be measured through the "iron triangle" model that includes time, scope, and cost. The success of a project should, therefore, be measured within project scope, scheduling, cost, quality, resource, and risk constraints in term of completing the project .

Scheduling is an important and difficult task during project planning since it helps to monitor the project duration and resource utilization. The challenge is about the scheduling complexity and dynamism: in fact, plans can change before the start but even during the implementation. In order to better manage projects and face the changes that may occur over time, a lot of methods were created, and among them, the Critical Path Method (CPM) is one of the better-known planning and control techniques in project scheduling.

The Critical Path Method

Proposed for the first time in 1956 during a collaboration between Morgan R. Walker (DuPont) and James E. Kelley Jr (Remington Rand), the Critical Path Method is a deterministic technique developed with the purpose of planning, managing, organizing and analyzing the total time involved in a project. The method attempts to establish the trade-off between the overall cost of the project and the total time for the completion of desired activities.

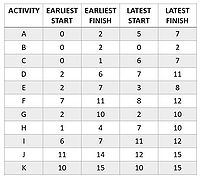
To perform this technique, it is fundamental the use of a network diagram to show logical relationships between the activities of a project, usually represented by arrows (activities) and nodes (beginning and end of the activities). CPM identifies the critical and non-critical paths on this precedence-relationship network, enabling managers to be more focused on those critical activities that can assure the project completion by the deadline. Minimum project duration can be estimated by using this algorithm, that can also provide parameters of activities including earliest starting time (ES), latest starting time (LS), earliest finish time (EF), latest finish time (LF), maximum available time and slack time, or total float.

In this regard, we can define:

• Earliest starting time (ES): the earliest time at which the task can start, given that its precedent tasks must be completed first;
• Earliest finish time (EF): the earliest start time for the task plus the time required to complete the task;
• Latest finish time (LF): the latest time at which the task can be completed without delaying the project;
• Latest starting time (LS): the latest finish time minus the time required to complete the task.

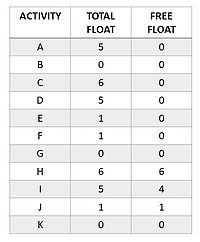
Moreover, two important concepts need to be explained: the total float and the free float. According to the PMBOK, the total float is the amount of time that a schedule activity can be delayed or extended from its early start date without delaying the project finish date or violating a schedule constraint, whereas the free float is the amount of time that a schedule activity can be delayed without delaying the early start date of any successor or violating a schedule constraint. The monitoring on these two floats is an important task for a project manager because they indicate the activities in the project that most constrain the schedule.

How to use the Critical Path Method

Activity list and network diagram

The Critical Path Method comprises several steps, but they can be summarized in three main phases:

1. Drawing the network diagram to show the existing relationships between activities to be performed in the project;
2. Estimating time involved in each activity;
3. Actual scheduling, checking the dependencies among activities and taking into account both necessary resources and available resources;

Step 1

Dummy activity example

The first step in CPM is constructing an arrow diagram that can show the precedence relationships among the project tasks.

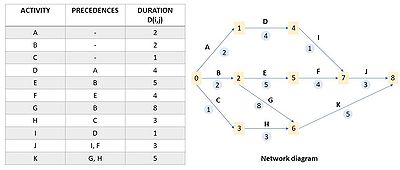
Generally, it starts by making a list of all the activities to be performed in the project, a list of the precedences and the relative duration. Based on this information, the network diagram can be constructed. Here, each arrow (capital letter) represents an activity; arrowheads show the order of each task. A node (number) indicates the beginning and the end of the activity; circled numbers stand for the duration of the activities.

ETE and LTE values

The construction basically follows four rules:

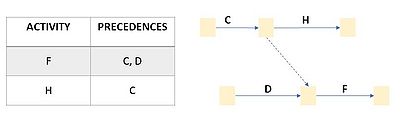
1. Each activity is represented by one arrow in the network;
2. "Dummy" activities (dotted arrows) are created whenever needed to portray the logic of the relationship between activities. A dummy activity represents an activity which takes no time and uses no resources;
3. Two activities shouldn't be identified by the same beginning event and by the same end event.
4. The following questions must be answered as each activity is added to the network, to ensure the network correctness:
   • What activities must be completed immediately before this activity can start?
   • What activities must follow this activity?

By applying these rules, the precedence-relationship diagram can be designed, and it will represent the master plan or working model of the entire project.

Step 2

ES, EF, LS and LF

Total float and Free float

The second step involves the calculation of the start and finish times for each activity. Using the duration shown in the previous list and the network that resulted from it, the earliest time event (ETE) and the latest time event (LTE) can be determined. The calculations of these times constitute, respectively, the forward pass and the backward pass. In the forward pass, computation begins from the start node and continues until the end node. For event 1, it is assumed that the ETE is equal to 0. Supposing that for an event i ETE(i) is known, ETE(j) for the event j can be calculated with

ETE(j) = max [ETE(i) + D(i, j)]

This calculation can be done for all the activities in the diagram. As an example from the network diagram:

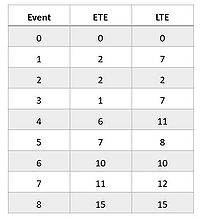
ETE(6) = max [1+3, 2+8] = 10

It is conventional to define the project time as the ETE of the end event; in this case, the project time is the minimum amount of time needed to finish the project.

In the backward pass, instead, the LTE of the end event is set equal to the project time. Thus, LTE(i) represents the latest time event i may occur, with the condition that the project time is still met. Supposing that for an event j succeding an event i LTE(j) is known, LTE(i) for the event i can be calculated with

LTE(i) = min [LTE(j) - D(i, j)]

As an example from the network diagram, since ETE(8) = LTE(8) = 15, there will be:

LTE(6) = min [15 - 5] = 10

LTE(7) = min [ 15 - 3] = 12

After completing the forward and backward passes, it is possible to determine the earliest starting time ES, latest starting time LS, earliest finish time EF, latest finish time LF, and float times for each activity. By convention, ES(i, j) = 0 for any activity that has no precedences, and LF(i, j) = project time for any activity that has no successors. ES(i, j) = ETE(i) because the activity (i, j) may begin as soon as all of its precedences are completed, and LF(i, j) = LTE(j) because the activity (i, j) must finish before event j occurs. Given these premises, EF(i,j) and LS(i,j) for each activity can be calculated with

EF(i, j) = ES(i, j) + D(i, j) = ETE(i) + D(i, j)

LS(i, j) = LF(i, j) - D(i, j) = LTE(j) - D(i, j)

As mentioned before, the total float TF and the free float FF can be calculated for each activity.

TF(i, j) = LTE(j) - ETE(i) - D(i, j) = LS(i, j) - ES(i, j)

FF(i, j) = ETE(j) - ETE(i) - D(i, j) = ETE(j) - EF(i, j)

If an activity in the network has minimal total float over all activities, then it's said to be critical. In the normal case, where the project time is chosen as the earliest possible finish time of the project, this activity has zero total float, whereas all other activities are noncritical. A critical path through the network diagram consists entirely of critical activities, that add up to the maximum duration of the project completion.

In the network diagram example, the critical path is composed of all the activities with total float equal to zero, which are activity B, activity G and activity K. In fact, the maximum duration of the project completion resulting from this path is

2 (B) + 8 (G) + 5 (K) = 15.

Step 3

The third step is about constructing a time chart that can display start and finish times for each activity and the associated floats. It may also show the relationships between activities, therefore presenting a possible project schedule. A schedule is possible in the sense that, if available resources are unlimited, the project could be completed at the scheduled time.

After plotting a time chart, it is also important a continuous monitoring and updating of both the plan and the schedule in order to better control the overall project.

The Resource-constrained Critical Path Method

So far, it has been explained briefly how to apply Critical Path Method to a project with specific tasks. However, the basic assumption of the CPM is that the resources required by the activities are unlimited, while some resources are highly limited in practice. Few studies have proposed heuristic algorithms to identify floats and the critical path by using resource-constrained scheduling (RCS) techniques. These traditional RCS techniques successfully generate resource-constrained schedules, in which all activities can be executed without resource constraints. However, they do not provide correct float data and the critical path of the schedules, since they don't consider the resource dependencies.