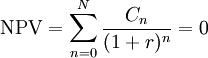Internal Rate of Return (IRR)

Developed by Pablo Leandro Capellari- s213666

Internal rate of return (IRR) is a parameter used in the financial analysis to determine the profitability of the investment, that is, it estimates the rate of return that the evaluated project could have. The term "internal" is because for the calculation of the IRR, external factors that could affect the profitability of the project, such as inflation, are not considered. In mathematical terms, the IRR is defined as the discount rate that causes the sum of the cash flows of the project to be zero. In other words, if the net present value (NPV) of a project is 0 at a certain rate, that rate is the IRR. Researchers in 2003 have validated the IRR as an alternative to the NPV as an indicator for project evaluation, considering that the IRR as from the point of view of the investor and the NPV from the point of view of the society. Its popular application is mainly because it defines the return on investment, sometimes seen as a measure of efficiency, beyond its documented limitations. For decision-makers, the IRR can be compared to the discount rate for rejecting or accepting projects. To be specific, for a project to be accepted, the IRR must be greater than the discount rate and when both are equivalent, a situation of indifference arises. To resolve many deficiencies related to the traditional IRR, some researchers have proposed to use the average internal rate of return (AIRR). The AIRR is based on the breakdown of the NPV of the project between the invested capital and the economic efficiency, maintaining the consistency of the NPV to decide the acceptance of a project. This breakdown generates valuable information helping to determine the uncertainty of a project allowing risk to be explored in more detail.

Big idea

It is possible to consider a successful investment as one that manages to reach or exceed the expected returns, and investors tend to analyze how this type of investment has behaved in the past to have a vision of what could happen in the future. It is clear that past performance is not a guarantee of what might happen in the future, but it is an important influence on financial attractiveness. If the cash flow turns out to be as predicted, that the asset was valued rationally, the investor gets the expected rate of return. On the other hand, if the return is higher than expected, the actual return will be higher than the target rate.Therefore, different types of rates can be defined: a) the required rate of return: which is the target rate measured at the beginning of the investment, b) the real rate of return: which is the rate measured at the end of the project. In the market, both rates are known as IRR.

IRR Mathematically

IRR is the discount rate (interest rate) that makes the sum of the present value of the cash flows zero. If the NPV of the project is zero at the selected discount rate, then that discount rate is, by definition, the IRR. IRR is algebraically equivalent. Mathematically expressed as:

$\operatorname{NPV} = \sum_{n=0}^N \frac{C_n}{(1+r)^n} = 0$

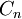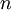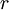where $C_n$ is a cash flow in period $n$ and $r$ is the IRR.

Practical example

In the following example, a highway construction project is outlined to demonstrate the calculation of IRR and other parameters. For exemplification purposes, the following data have been used: The project opens in year 0 and has an evaluation period on 10 years, the project has the following first year impacts: –Time savings: 500,000 DKK. –Accident savings: 50,000 DKK. Operation and maintenance: 100,000 DKK.

Assumptions

Discount rate	0,03
Traffic growth	0,015
Price growth	0,01

In addition, different reference values have been used for this type of project, such as a discount rate of 3%, annual traffic growth of 3% and price growth of 1%.

Year	-	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10
Discount factor	-	1,09	1,06	1,03	1,00	0,97	0,94	0,92	0,89	0,86	0,84	0,81	0,79	0,77	0,74
Traffic growth	-	0	0	0	1,00	1,02	1,03	1,05	1,06	1,08	1,09	1,11	1,13	1,14	1,16
Price growth	-	0	0	0	1,00	1,01	1,02	1,03	1,04	1,05	1,06	1,07	1,08	1,09	1,10
Construction costs	,-10.612.090	-3.642.423	-3.536.333	-3.433.333
Scrap value	7.440.939
Operation and maintenance	-953.020	-	-	-	-100.000	-97.087	-94.260	-91.514	-88.849	-86.261	-83.748	-81.309	-78.941	-76.642	-74.409
Time savings	5.372.322	-	-	-	500.000	497.646	495.302	492.970	490.649	488.338	486.039	483.750	481.473	479.205	476.949
Accidents	476.510	-	-	-	50.000	48.544	47.130	45.757	44.424	43.130	41.874	40.655	39.470	38.321	37.205
NPV	1.724.661
BCR	1,16
IRR	4,57%
(Simple example of the calculation of the IRR. Developed by Pablo Capellari s213666)

The table displays year-over-year cash flows, plus calculations for Residual Value, Net Present Value (NPV), Benefit Cost Rate (BCR), and Internal Rate of Return (IRR). For the calculation of the IRR, the Excel function "Goal Seek" has been used, where it allows estimating the IRR generating an NPV=0. Another option that can be used to calculate the IRR is the =IRR(cash flows) function in Excel.

Negative IRRs

In simple terms, a negative IRR indicates that the cash flows of a project are not enough to cover the initial investment. Therefore, this means that the project is not attractive to the investor because he would lose money. In such situations, the NPV would also be negative. On the other hand, a negative NPV value does not always mean a negative IRR, it just means that the discount rate is greater than the IRR. The following simple example allows us to clarify the concept of negative IRR.

Year	Year 0	Year 1	Year 2	Year 3	Year 4
Cash Flow	.-300.000,00 kr.	30.000,00 kr.	35.000,00 kr.	50.000,00 kr.	80.000,00 kr.
IRR	.-13%
(Simple example of the calculation of a negative IRR. Developed by Pablo Capellari s213666)

Application

IRR in real-estate investment

It is common opinion that the Internal Rate of Return (IRR) may be the real estate industry's preferred performance measure as a means of evaluating the return on projected investments. However, finance textbooks pointed out that the net present value (NPV) is a superior method to the IRR used to evaluate potential investments, however, in practice, the internal rate of return return still dominates. This is an easy-to-understand indicator that the appeal is that it meets the need for a single number compared to other opportunities or benchmarks. This simplicity belies its true nature and many of the problems that can arise when it is used to evaluate capital investment projects.

IRR limitations on real state investments

• Does not express a measure of the size or timing of the project.

• Does not differentiate between sales revenues or cash flows from operations.

• Does not demonstrate the timing of cash flows.

• Assume cash flows can be reinvested.

• Does not differentiate risk levels between years within the project.

• No express leverage risk.

• Not influenced by real estate, lease, operating or liquidity risk.

LIMITATIONS

The IRR is generally used by decision makers to choose which of the investment alternatives is the most attractive, unfortunately this rate has several defects: (1) the same project may have more than one IRR, (2) complex value IRRs may arise; (3) is generally incompatible with the NPV for decision making; (4) IRR ranks projects differently than NPV (5) is not applicable on variable costs of capital.

Multiple IRRs

Graph of two IRRs. Developed by Pablo Capellari s213666

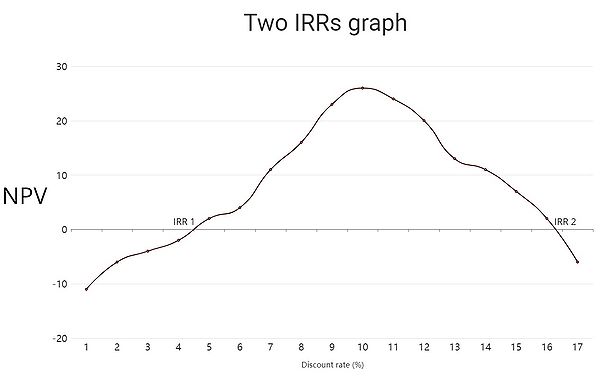
Generally speaking, projects start with a negative cash flow, which then turns into a series of positive cash flows. For example, in the case of real estate investments, the cash flow starts negative due to the purchase of the property and over the years it becomes positive due to the income from rentals or eventual sales. This typical situation generates a change in the "direction" of the cash flows, it generates a unique IRR. But in many other projects, this change of "direction" occurs repeatedly due to negative and positive cash flows being produced alternately, this effect generates what is commonly known as multiple IRRs. To continue with the example of real estate investments, this could be the situation where it is invested in some improvements to the property which generates negative cash flows.

The use of the IRR is popularly accepted for single IRR projects, because this rate clearly defines the return on an investment, being a measure of project efficiency. However, these assumptions must be carefully considered in projects with multiple IRRs.

The graph on the right represents a project with two IRRs, the first (IRR1) of 4.7% and the second (IRR2) of 16.4%. The net present value (NPV) is represented on the vertical axis and the discount rate (%) on the horizontal axis.