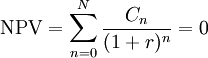Internal Rate of Return (IRR)

Developed by Pablo Leandro Capellari- s213666

Internal rate of return (IRR) is a parameter used in the financial analysis to determine the profitability of the investment, that is, it estimates the rate of return that the evaluated project could have. The term "internal" is because for the calculation of the IRR, external factors that could affect the profitability of the project, such as inflation, are not considered. In mathematical terms, the IRR is defined as the discount rate that causes the sum of the cash flows of the project to be zero. In other words, if the Net Present Value (NPV) of a project is 0 at a certain rate, that rate is the IRR. Researchers in 2003 have validated the IRR as an alternative to the NPV as an indicator for project evaluation, considering that the IRR as from the point of view of the investor and the NPV from the point of view of the society. Its popular application is mainly because it defines the return on investment, sometimes seen as a measure of efficiency, beyond its documented limitations. For decision-makers, the IRR can be compared to the discount rate for rejecting or accepting projects. To be specific, for a project to be accepted, the IRR must be greater than the discount rate and when both are equivalent, a situation of indifference arises. To resolve many deficiencies related to the traditional IRR, some researchers have proposed to use the average internal rate of return (AIRR). The AIRR is based on the breakdown of the NPV of the project between the invested capital and the economic efficiency, maintaining the consistency of the NPV to decide the acceptance of a project. This breakdown generates valuable information helping to determine the uncertainty of a project allowing risk to be explored in more detail.

BIG IDEA

It is possible to consider a successful investment as one that manages to reach or exceed the expected returns, and investors tend to analyze how this type of investment has behaved in the past to have a vision of what could happen in the future. It is clear that past performance is not a guarantee of what might happen in the future, but it is an important influence on financial attractiveness. If the cash flow turns out to be as predicted, that the asset was valued rationally, the investor gets the expected rate of return. On the other hand, if the return is higher than expected, the actual return will be higher than the target rate.Therefore, different types of rates can be defined: a) the required rate of return: which is the target rate measured at the beginning of the investment, b) the real rate of return: which is the rate measured at the end of the project. In the market, both rates are known as IRR.

General usage of IRR

As mentioned earlier, the IRR is a investment decision-making tool used to determine the viability of various investment options. The general criteria for understanding suitability for a project are as follows:

• if TIR > r $\rightarrow$ project is accepted. The reason for this is that the project generates a higher rate of return than the required minimum rate of return (opportunity cost), which means we will make more money than investing in a specific project (IRR), for example, buying government bonds.

• If TIR < r $\rightarrow$ project will be rejected. The reason is that the project's return is lower than the required minimum return. This shows that if we invest in government bonds (r), we will make more money than if we invest in specific projects (IRR).

• If TIR = r 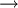$\rightarrow$ it would be a situation of indifference, similar to the one that occurs when the NPV is equal to zero.

IRR Mathematically

IRR is the discount rate (interest rate) that makes the sum of the present value of the cash flows zero. If the NPV of the project is zero at the selected discount rate, then that discount rate is, by definition, the IRR. IRR is algebraically equivalent. Mathematically expressed as:

$\operatorname{NPV} = \sum_{n=0}^N \frac{C_n}{(1+r)^n} = 0$

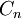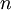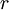where $C_n$ is a cash flow in period $n$ and $r$ is the IRR.

Practical example

In the following example, a highway construction project is outlined to demonstrate the calculation of IRR and other parameters. For exemplification purposes, the following data have been used: The project opens in year 0 and has an evaluation period on 10 years, the project has the following first year impacts: –Time savings: 500,000 DKK. –Accident savings: 50,000 DKK. Operation and maintenance: 100,000 DKK.

Assumptions

Discount rate	0,03
Traffic growth	0,015
Price growth	0,01

In addition, different reference values have been used for this type of project, such as a discount rate of 3%, annual traffic growth of 3% and price growth of 1%.

Year	-	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10
Discount factor	-	1,09	1,06	1,03	1,00	0,97	0,94	0,92	0,89	0,86	0,84	0,81	0,79	0,77	0,74
Traffic growth	-	0	0	0	1,00	1,02	1,03	1,05	1,06	1,08	1,09	1,11	1,13	1,14	1,16
Price growth	-	0	0	0	1,00	1,01	1,02	1,03	1,04	1,05	1,06	1,07	1,08	1,09	1,10
Construction costs	,-10.612.090	-3.642.423	-3.536.333	-3.433.333
Scrap value	7.440.939
Operation and maintenance	-953.020	-	-	-	-100.000	-97.087	-94.260	-91.514	-88.849	-86.261	-83.748	-81.309	-78.941	-76.642	-74.409
Time savings	5.372.322	-	-	-	500.000	497.646	495.302	492.970	490.649	488.338	486.039	483.750	481.473	479.205	476.949
Accidents	476.510	-	-	-	50.000	48.544	47.130	45.757	44.424	43.130	41.874	40.655	39.470	38.321	37.205
NPV	1.724.661
BCR	1,16
IRR	4,57%
(Simple example of the calculation of the IRR. Developed by Pablo Capellari s213666)

The table displays year-over-year cash flows, plus calculations for Residual Value, Net Present Value (NPV), Benefit Cost Rate (BCR), and Internal Rate of Return (IRR). For the calculation of the IRR, the Excel function "Goal Seek" has been used, where it allows estimating the IRR generating an NPV=0. Another option that can be used to calculate the IRR is the =IRR(cash flows) function in Excel.

Negative IRRs

In simple terms, a negative IRR indicates that the cash flows of a project are not enough to cover the initial investment. Therefore, this means that the project is not attractive to the investor because he would lose money. In such situations, the NPV would also be negative. On the other hand, a negative NPV value does not always mean a negative IRR, it just means that the discount rate is greater than the IRR. The following simple example allows us to clarify the concept of negative IRR.

Year	Year 0	Year 1	Year 2	Year 3	Year 4
Cash Flow	.-300.000,00 kr.	30.000,00 kr.	35.000,00 kr.	50.000,00 kr.	80.000,00 kr.
IRR	.-13%
(Simple example of the calculation of a negative IRR. Developed by Pablo Capellari s213666)

The sum of the cash flows is negative, so it generates a negative IRR, in this case the initial investment is 300.000,00 kr (Danish kroner) and the income in the four-year period adds up to a total of 195.000,00 kr (Danish kroner), for so the IRR is -13%.

APPLICATION

IRR in real-estate investment

It is common opinion that the Internal Rate of Return (IRR) may be the real estate industry's preferred performance measure as a means of evaluating the return on projected investments. However, finance textbooks pointed out that the net present value (NPV) is a superior method to the IRR used to evaluate potential investments, however, in practice, the internal rate of return return still dominates. This is an easy-to-understand indicator that the appeal is that it meets the need for a single number compared to other opportunities or benchmarks. This simplicity belies its true nature and many of the problems that can arise when it is used to evaluate capital investment projects.

IRR limitations on real state investments

• Does not express a measure of the size or timing of the project.

• Does not differentiate between sales revenues or cash flows from operations.

• Does not demonstrate the timing of cash flows.

• Assume cash flows can be reinvested.

• Does not differentiate risk levels between years within the project.

• No express leverage risk.

• Not influenced by real estate, lease, operating or liquidity risk.

IRR vs NPV for project ranking

In situations where it is necessary to choose between mutually exclusive projects, it can usually happen that there are differences in the results of the analyzes between the NPV and the IRR, which often causes problems for decision-makers. The use of the IRR is disputed for various reasons, but it is still widely used in practice . The IRR tends to express the return on invested capital, a project should be accepted if the IRR is greater than the interest rate, because this case would generate a positive NPV . This means that for these situations both indicators are consistent and the acceptance of a single project would be facilitated. For mutually exclusive projects, where these indicators rank in a different order than the alternatives, it is usually explained by the "investment assumption", which establishes that the differences between intermediate cash flows must be recognized. For these situations, the investor must consider what will happen to the differences in cash flows in between. For example, if project A has an initial investment of 200,000 kr (Danish kroner) and another project B an initial investment of 150,000 kr (Danish kroner), the decision-maker must consider what happens with that difference of 50,000 kr (Danish kroner). It is assumed that in this example, the NPV calculation is higher in project B, while the IRR is higher in project A. Therefore, the investor will have uncertainty between both projects, depending on whether to rely on the criterion of NPV or IRR. This author proposes the use of the Investment Difference (DI), by which it is intended to compare the cash flows of mutually exclusive projects.

LIMITATIONS

The IRR is generally used by decision makers to choose which of the investment alternatives is the most attractive, unfortunately this rate has several defects:

Mutually Exclusive Projects

This limitation is related to the "IRR vs NPV for project ranking" section because if it is the only indicator used, this could cause erroneous decisions when choosing a project. This type of problem arises when the projects have different values ​​of initial investment, let's suppose project A with an initial investment of 10,000 kr, an NPV of 80,000 kr, and an IRR of 100%. On the other hand, a project B with an initial investment of 100,000 kr, an NPV of 360,000 kr, and an IRR of 50%. Considering the IRR criterion alone, the investor could decide on project A (IRR=100%), but project B (IRR=50%) would generate 280,000 kr more. It is to be expected that in a project with higher investment, the profits are also higher. The analysis would be to invest 10 times in project A with the same investment used for project B, of course, if this were feasible. From another point of view, focusing the analysis on the NPV over the IRR would generate discarding the most profitable in percentage terms. A practical alternative to solve this situation from different perspectives is normalizing both projects, that is, dividing the cash flow of project B 10 times.

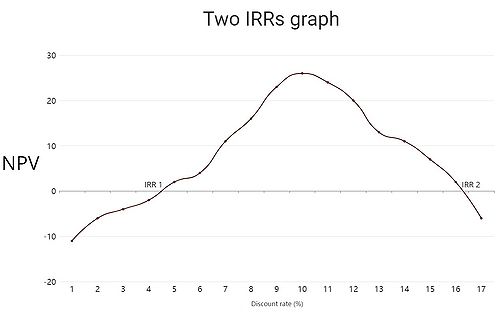
Multiple IRRs

Graph of two IRRs. Developed by Pablo Capellari s213666

Generally speaking, projects start with a negative cash flow, which then turns into a series of positive cash flows. For example, in the case of real estate investments, the cash flow starts negative due to the purchase of the property and over the years it becomes positive due to the income from rentals or eventual sales. This typical situation generates a change in the "direction" of the cash flows, it generates a unique IRR. But in many other projects, this change of "direction" occurs repeatedly due to negative and positive cash flows being produced alternately, this effect generates what is commonly known as multiple IRRs. To continue with the example of real estate investments, this could be the situation where it is invested in some improvements to the property which generates negative cash flows.

The use of the IRR is popularly accepted for single IRR projects, because this rate clearly defines the return on an investment, being a measure of project efficiency. However, these assumptions must be carefully considered in projects with multiple IRRs.

The graph on the right represents a project with two IRRs, the first (IRR1) of 4.7% and the second (IRR2) of 16.4%. The net present value (NPV) is represented on the vertical axis and the discount rate (%) on the horizontal axis.

IRR Incalculable

The impossibility of calculating the IRR is one of the most important criticisms of this indicator. One of the situations where this problem occurs is in projects where all cash flows are positive, which rarely happens in practice (it implies output, without input). Another situation where the IRR is not calculable is when all cash flows are negative. It is clear that in these two situations there is no doubt whether the project should be accepted or rejected. The third circumstance where IRR cannot be calculated is when net cash flow is zero.

Reinvestment

This limitation of the IRR is based on the "investment assumption", and this is because the IRR assumes that the positive flows generated by the project are reinvested at the IRR, not at the discount rate. And the negative flows should divest the project but these are not considered to simplify the calculation. To correct inconsistencies arising from the use of implicit assumptions, simply make them explicit. For example, if it is necessary to know what the internal rate of return of the reinvested cash flow is at the discount rate, do the calculation twice. The second time, enter the actual cash flow generated by reinvested funds for all projects. If funds are available to pay off the debt, the avoided interest is included in the project's positive cash flow. Of course, it is essential to treat all projects equally in this regard if meaningful comparisons are to be made. While this technique would have been cumbersome when writing some of the most popular textbooks decades ago, modern electronic tools make it easy. However, this adjustment is usually unnecessary. In general, reinvesting at the IRR is a reasonable assumption. This is done in the matter of bond yields, which is ultimately an investment decision.