Network Planning in Project Management

Abstract

Planning is a big part of project management, and the success of it is highly dependent on this process. The method Network planning will be used to reduce possible complexity of a project and smoothen the execution of the project planning. A project of a large scale that require coordination of multiple activities is a challenging task for a project manager. Succeeding a project is about simple forms of working and organising regardless the size of the project. The method will therefore be used as an integration approach where the different activities are separated to get an overview of the process. Understanding the dependencies of the project and setting up millstones is also ideal to motivate the employees involved in the project.

Project networking is investigating a project as sets of interconnected activities with the purpose of assisting in planning, managing, and controlling projects . This article will mainly focus on the most well know network planning techniques: the Critical path method (CPM) and the Program evaluation and review technique (PERT). CPM and PERT was developed in the 1950’s and has since then been used widely in operation research . The goal of the tool is to manage a project, meeting its deadlines with a minimum total cost. The tools will help organising the project, getting an overview of the activities and estimate the total length of the project. There can be multiple paths to the end of the project, but those tools can help the manager find the most effective one. Initially the methods will need three types of information to describe the project: activity, precedence, and time . This will be elaborated in the article followed by a description of the tool, an example of how to use the tool, other alternative planning tools and the limitations of the tool.

This article will elaborate the theory behind network/graphs and the focus on the comparison of different planning tools that are not focused on network planning specifically. The article is based on a project managers point of view and what that person may consider and wonder about when planning a project.

About

Network planning is a tool used in project, program and portefolio management in the planning process. The tool is great to give an overview and coordinate the activities in the given project in order to help project managers. Today it is set up as a software package in order to deal with the data and the progress. The two tools that will be described and elaborated in this article is CPM and PERT, which were originally independently developed, but today widely used as two tools merged into one . The tools work great together combining the techniques from both. This is also the case for most softwares, that it uses both tools in one with the purpose of scheduling and monitoring the project planning. In general network planning can study many different kind of problems such as project scheduling, risk analysis, cost minimization or Net Present Value maximization depends on the information that is needed.

Network Theory

The first section will describe the terminology of network planning where two important definitions are described.

Graph Theory

A graph that consists of multiple nodes and arcs are considered a network. This means that a network consists of nodes that are connected through arcs. In this article the exploration of networks will be centered around project planning, which means that the nodes correspond to the events in the project. The arcs correspond to the connection between the events and can be either directed or undirected. When an arc is directed, for example for A to B, it means that the network can only go from A to B and not from B to A. An example of a network is illustrated below.

Figure 1

Spanning Tree

Consider a network with a number of nodes n and no initially arcs. By adding one arc at a time between the nodes, a tree will appear. The first arc can be between any of the nodes in the network, but along the way, an arc cannot be placed if it creates a cycle. A network of nodes connected through arcs are referred to as a spanning tree. A network therefore differs between being cyclic or acyclic

CPM/PERT

The CPM/PERT method is an ideal too to get an overview of a project planning process and help answering multiple questions that a project manager may have for the process.

Initial work

As mentioned earlier, some information is needed in order to use network theory for planning a project:

1. Activity information: the project must be broken down into individual activities

2. Precedence relationships: find immediate predecessor(s) for each activity

3. Time information: know/estimate the duration of each activity

Other than that, a network will have one or more start node(s) and a finish node/node(s).

A project network can be split into two, depending on whether the activity is on the node or on the arc. Those two types are referred to Activity-on-arc (AOA) and Activity-on-node (AON). For the AOA, the node is separating the activities and therefor the arcs show the precedence relationship between the activities on the nodes. The AON is used in the CPM/PERT that will be elaborated later in this article. The AON method is remarkable more simpel to construct, understand and revise than the AOA. Therefor this article will forward going only focus on AON.

Critical Path

The critical path is a part of the project planning method that can answer how long time the project will take to complete and what are the bottlenecks to be aware of in order to prevent delays of the whole project?

The critical path will establish the time length of the project, summing over all the durations of the activities. In a project network from a starting node to an end node, multiple paths can be set up if the activities can be done in sequence with a predecessors and no overlap. Therefor some activities have to wait for other activities to finish before it can start. Those can be activities that are on another path. The path with the longest total duration time is the critical path and therefor the longest duration time that the project can take assuming no delays occur. This is also the bottleneck activities of the project where delays most be avoided so that the whole project can be completed in time. The activities in the critical path therefor deserves the most attention, since this is very important for the project.

Scheduling

Earliest start- and finish time

The next question from the project manager is, when all the individual activities at earliest can start and finish? The first step of the procedure is therefor to address when every activity in the process can start and end if no delays occur. Those are defined as earliest starting time (ES) and earliest finish time (EF), where EF is equal to ES plus the estimated duration for the given activity. For convenience, the times are estimated in time periods instead of dates. This article will be based on weeks, but it could also be months or years.

How to find ES

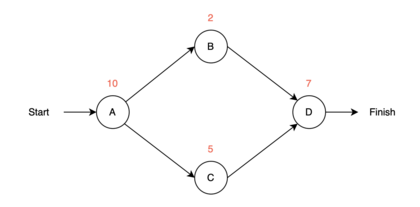
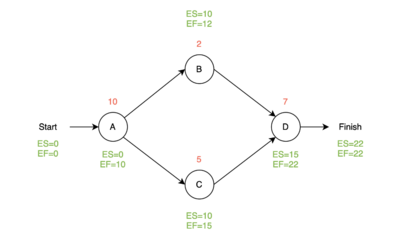
The first activity will always start at time period 0. lets call the first activity A with a duration of 10 weeks. Then ES_A=0 and EF_A=0+10=10. For the next two nodes, lets call them B and C with duration 2 and 5 weeks, then ES_B=10 and EF_B=10+2=12 and ES_C=10 and EF_C=10+5=15. For the last node/activity of this small example, let's call it D with a duration of 7 weeks, the activity will have 2 predecessors and cannot start before both of them are done. Therefor the earliest starting time for C will be 15 weeks instead of 12. This means that ES_D=15 and EF_D=15+7=22. Now we know ES and EF for all nodes. The small example is illustrated in the figure 2.

Figure 2

If a node/activity has a single predecessor, then ES for the activity is equal to EF for the predecessor. If the activity has two predecessors then ES is equal to the latest finished predecessors ES.

In the small example from above this the critical path drawn together with ES and EF in figure 2. Notice that this example has two possible paths where the first one has a total time length of 19 and the second one has a total time length of 22.

$Start \rightarrow A \rightarrow B \rightarrow D \rightarrow Finish$

$Start \rightarrow A \rightarrow C \rightarrow D \rightarrow Finish$

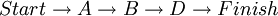
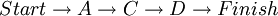
Since the second path has the longest duration, this is the critical path.

Figure 3

Latest start- and finish time

Another question, the project manager could ask, is how much the individual activities can be delayed, before the whole project is delayed. To answer this question, the next step is to calculate the latest start time (LS) and the latest finish time (LF) for every activity, where LS is equal to LF minus the estimated duration of the given activity. The times are still based on time period, for example weeks.

How to find LF

When those parameters are estimated the procedure is to start backwards in the network. The method assumes that an activity's successors cannot start before the given activity is done.

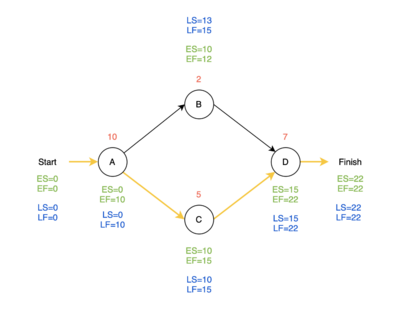
For the finish node LF will always be equal to ES, so that the project is still completed within the estimated time frame. LS is then equal LF minus the duration time, which is 0 for the finish node. The explanation of how to find LS and LF will again use the small example from before. This means that the next step is to find LS and LF for activity D, LF_D=22 and LS_D=22-7=15. This continues for the rest of the nodes until Start. Node A has two successors and therefor LF is equal the lowest value of the B and C's LS, which is 10 instead of 13. All the blue values therefor indicates that last possible chance for an activity to finish before the whole project will be delayed.

Figure 4

Slack in the schedule

It is noticeable that node B is the only node with a different LS and LF value than ES and EF. To understand what this means for the project, is slack investigated in the schedule. The slack is calculated using LF and EF for every activity:

$Slack = LF - EF$

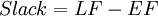
Calculating that slack for all 4 nodes, the only node with a slack different from 0 is B.

$Slack_B = LF_B - EF_B = 15-12 = 3$

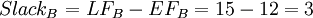
This means that activity B can be delayed with up to 3 weeks and the project will still be completed within the estimated time frame of 22 weeks. This also means that the nodes A, C and D with a slack value of 0 cannot be delayed without delying the whole project. Those nodes are therefor also forming the critical path, which is illustrated with a yellow line in figure 4. This is how the PERT/CPM method identifies the critical path.

Expanding the method

This article is narrowed down only looking at the time aspect of project network planning, but there is more of the tool to investigate. The method may be expanded to uncertainty and costs which are also very important aspects of project planning.

The method is using accurate estimations of activity duration, which is associated with some uncertainty. Therefor it is very relevant for the project manager to know what the probability is to meet the deadline. The uncertainty is then expanded to include time-costs trade offs. So if it possible to decrease uncertainty with increased cost. This part of the method will not be further investigated in this article.

Limitations

Going through the possible questions of a project manager, this tool is indeed a great tool to answer the questions represented in this article. On the other hand, this tool does have some limitations to be aware of. The tool is great to visualise those small examples, but it will be more difficult to use it with big complex projects where the time estimations and predecessors are hard to identify. It can rapidly become a very time consuming task to draw up the diagram and make the scheduling calculations for every activity. To solve this on larger problems, you may have to use linear programming, but that can also be very complex and time consuming to set up.

It is a very simple method, which makes is great to answer the questions that are asked in this article, but there is also a lot of other questions that the method does no answer. It i focused on the time aspect, but not on any resources of the project. This is causing a lot of inflexibility for the process and may not work on the longer term projects.

Alternative planning tools

Since all project planning tools have pros and cons, this method may be more relevant for some projects and some other methods may work for the other projects. Other examples of project planning tools are Gantt Charts and Milestone Planning.

If the project manager wants to get a better overview of the resources in a project, which the CPM/PERT does not include, the Gantt Charts is a great alternative. With the Gantt Charts it is easy to follow how the resources are utilised. The Milestone Planning method is a great reactive tool to evaluate on the progress of the project. At the same time, this tool seems more simple than the CPM/PERT and would therefor be easier to use on big projects.

Evaluation

Taken the limitations of the tool into account, the PERT/CPM is still one of the most widely used OR techniques used by project managers. Even though the tool does not answer all the questions that a project manager may have, the answers that it does give, are very usefull. Also a lot of software package is already installed on many workstations in order to use this tool. This tool is applicable for many projects even though other great project planning tools are available too. Which tool to choose is highly dependent on preferences and the complexity of the projects. It is important to notice that all the project planning tools is intended to reduce complexity of a project and it is therefor important to choose the correct tool so that it doesn't have the opposite effect. This tool could as well be applied for program or portfolio management.

Annotated Bibliography

If you find this topic interesting, some articles are presented in order to dig deeper into the subject: