Net Present Value (NPV) - Discounted cash flow

Abstract

Net Present Value (NPV) and Discounted Cash Flow (DCF) are two financial concepts, strongly connected to each other. So closely connected that the Net Present Value is a technique based on Discounted Cash Flows. Both these concepts operate under the time value of money (TVM) principle, which assumes that money is worth more today than it is in the future. When making a project, program or portfolio decision, the NPV rule emerges as one of the of the most commonly used financial metrics.

On the one hand, Discounted Cash Flow (DCF) is a valuation method that estimates the attractiveness of an investment project or the value of a company based on their projected cash flows discounting them to the present. A DFC analysis involves forecasting future cash flows that a project or investment is expected to generate, and then discounting those values back to the present using a discount rate or required rate of return. This technique is the most widely used practice for evaluating capital projects, being they acquisitions of companies or the purchases of machines.

On the other hand, Net Present Value (NPV) is a valuation method used to evaluate investment projects. It relies on the estimated future cash flows of for the project discounting them to the present value, allowing a comparison with the initial investment. By accounting for startup costs ad discounting future cash flows, NPV determines the net return on the investment. As it takes into consideration the time value of money and provides a concrete number (rates of return for the investment) that managers can use easily compare when making decisions.

As can be assumed from the previous lines, the calculation of discounted cash flows for future years becomes critical for the investment decision, when it is based on the net present value of the considered project.

The article is structures explaining relevant concepts (Time Value of Money, Discount rates), explaining the connection between Net Present Value and Discounted Cash Flows, followed by an analysis of the different ways of creating discounted cash flows. Advantages and disadvantages are also considered and presented. At the end, the article briefly highlights the key references used.

Big Idea

As stated in the abstract, the financial methods being considered in this report are strongly connected to each other. The NPV approach consists in discounting all future cash flows (both in- and out-flow) resulting from the project or investment opportunity under consideration with a given discount rate and then summing them together.

A core principle for the mentioned methods is the Time Value of Money, a concept that expresses how money is worth more today than tomorrow. The second relevant concept is the discount rate used to determine the present value of future cash flows in NPV calculation. The choice of the discount rate can dramatically change the NPV since the NPV is an inverse function of the discount rate, so it has to be carefully selected. It requires careful consideration of various factors, including the risk profile of the investment, the company's cost of capital and the expected return on alternative investments.

Time Value of Money

$1 of today is worth more than $1 of tomorrow

Time value of money (TVM) is a core financial principle that states a sum of money is worth more now than it will be in the future. . This is because when the investor has the money available, it can be re-inverted generating more profits. Money available at different points in time has different values, which means that a sum of money’s value depends on how long you must wait to use it. The sooner you can use it, the more valuable it is.

TVM plays a crucial role in investment analysis, particularly when assessing future cash flows and expected investment returns. Investors rely on this concept to assess businesses’ present values based on projected future returns, which helps them decide which investment opportunities to prioritize and pursue. When investment options vary in time horizons, the TVM helps in determining the most profitable choice based on the present and future value of the money invested.

Discount Rate

Figure 1: NPV vs. Discount rate (i). Own creation inspired from .

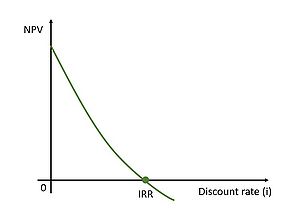
In corporate finance, a Discount Rate is the rate of return used to discount future cash flows back to their present value. It takes into consideration the time value of money and the risk associated with an investment. In other words, the discount rate is the interest rate used to convert future cash flows into their equivalent value in today’s dollars.

When selecting a discount rate for an investment project, it's crucial to remember that the Net Present Value (NPV) is an inverse function of the rate. In other words, as the interest rate increases, the NPV decreases. This highlights the importance of selecting the appropriate discount rate, as it can significantly impact the calculated NPV for the project. As observed in the image, the discount rate that gives a zero NPV is defined as the Internal Rate of Return (IRR). The IRR is a profitability measure that depends solely on the amount and timing of the project cash flows.

When making project, program or portfolio management decisions, this rate value is often defined as the minimum acceptable rate of return that investors deem acceptable on an investment. The discount rate is determined by assessing the cost of capital, risks involved, opportunities in business expansion, rates of return for similar investments or projects, and other factors that could directly affect an investment or project under consideration.

Here, two of the most widely used methods for defining the discount rate are presented:

• Cost of Capital: is the minimum required rate of return that an investor expects to earn on an investment to compensate the risk associated to it. The cost of capital is often used as a discount rate for evaluating investments that are similar in risk to the overall operations of the company.
• Weighted Average Cost of Capital (WACC): WACC is a specific type of cost of capital where the cost of each type of capital is weighted by its percentage of total capital and they are added together. WACC is often used as a discount rate for projects or investments that are expected to have a similar risk profile as the overall operations of the company.

As a general rule it can be said that Cost of Capital can be used as a discount rate when analyzing a particular investment. Whereas, the WACC is considered as a discount rate when considering a project as part of the portfolio of a company.

Net Present Value (NPV)

The Net Present Value can be defined as the present value of the investment. It compares future net cash flows discounted to its present value, with the initial investment of the project. The result obtained, represents the increase in the wealth of the investor along the time. As previously mentioned, the NPV analysis accounts for the time value of the money and can be used to compare different investment projects being under consideration. The discount rate used to discount the cash flows is defined for each project under analysis and is associated with the investment risk profile. Riskier projects are discounted heavily.

In corporate finance, the Net Present Value analysis is one of the tools that investors use when comparing investment projects and deciding which one to pursue. This method provides a concrete number that managers can use to easily compare an initial outlay of cash against the present value of the return.

NPV combines projections of all net cash flows to assess the overall value of a project from the present view. Therefore the NPV is given by :

$N P V=\sum_{t=0}^{n} \frac{N C _{t}}{(1+i)^{t}}$

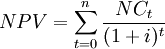
The difference between the cash inflows and cash outflows, gives the net cash flow, 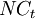$N C _{t}$ of the corresponding period. For investments which are characterized by initial investment, 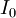$I_{0}$, subtracting it from the present value of the net cash flows gives the net present value. If a possible final payment, 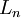$L_{n}$, for the liquidation of the investment in t = n is also considered, the NPV can be calculated as follows :

$N P V=-I_{0}+\sum_{t=1}^{n} \frac{N C _{t}}{(1+i)^{t}}+\frac{L_{n}}{(1+i)^{n}}$

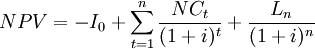
The outcome of this method can be either positive or negative. A positive outcome could signify a worthwhile investment, resulting in a profitable return, whereas a negative value would indicate that the project’s return is not enough to make it profitable. A decisión rule is defined for the outcome obtained from the calculation of the NPV.

• If the Net Present Value (NPV) is positive (NPV > 0), it means that the benefits deriving from the investment opportunity exceed the costs in the amount of the NPV. In this case, then the investment deserves to be made.
• On the contrary, a negative result (NPV < 0), will imply that the discounted cash flows doesn’t cover the initial investment generating a decreased profit in an amount equal to the negative NPV. In these cases, the investment can be rejected.
• If NPV = 0, it means that the sum of the cash flows discounted to their present value are equal to the amount of the initial investment. In this case, the opportunity doesn’t generate profits or losses and other decision criteria should be implemented.

Discounted Cash Flow (DCF)

Discounted Cash Flow (DCF) is a valuation method that helps to estimate what an asset is worth today by using expected future cash flows. It uses future free cash flows projections (FCF) discounting them to get a present value that can be used to estimate the potential for an investment. The discount rate used when discounting the cash flows, reflects the risk associated with their estimation. A DCF analysis reports how much money can be spent on the investment in the present in order to get a desired return in the future. It can be used to calculate the value of another business, stock, real state, equipment or any long term asset. This method operates under the time value of money principle and can be used to determine if in an investment or project is worthwhile comparing it to other alternatives. The mentioned analysis can be applied to value a stock, company, project, and many other assets or activities, and thus is widely used in both the investment industry and corporate finance management.

The basic model valuation is given by:

$Value=\sum_{t=1}^{n} \frac{C F _{t}}{(1+r)^{t}}$

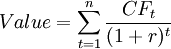
Where 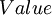$Value$ refers to the value of the asset; 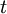$t$ is the time period and ranged from 1 to n; 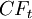$C F _{t}$ is the cash flow in period t; and 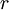$r$ represents the discount rate. According to the model, the value of any asset is the present value of its expected cash flows.

DCF valuation models

As stated earlier in this article, the projected cash flows of a firm or project become highly relevant for the NPV analysis. According to this, three basic DCF models can be identified and are :

• Dividend Discount Model (DDM)
• Free Cash Flow to Equity (FCFE)
• Free Cash Flow to Firm (FCFF)

Bibliography

Brealey, R., Myers, S., Allen, F., Principles of Corporate Finance, 10th edition, McGraw-Hill Irwin, 2010

Chapter 5 in this book presents the Net Present Value as investment evaluation criteria and compares is with other financial metrics, such as payback period and book rate of return. It also highlights the need for more accurate methods when making substantial capital investment decisions. It presents the expected rate of return rule as an alternative to calculating NPV, and discusses its advantages and potential pitfalls.

Žižlavský O., Net present value approach: method for economic assessment of innovation projects., 19th International Scientific Conference, Economics and Management, (2014), pp. 506-512

The research paper provides a comprehensive understanding of the NPV method for project appraisal. It emphasizes the importance of the time value of money and selecting an appropriate discount rate. This paper serves as a valuable resource for anyone seeking to gain insights into the NPV approach.

Ferrari, C., Bottasso, A., Conti, M. and Tei, A., Ch. 5 - Investment Appraisal. In: Economic role of transport infrastructure: Theory and models (2018), pp. 85-114

Chapter 5 covers financial appraisal methods, highlighting the importance of net present value (NPV) and its relationship with discount rates. It stresses the need to select appropriate discount rates when appraising projects using NPV and introduces sensitivity analysis as a crucial tool for accurate financial evaluations. Overall, the chapter provides readers with the necessary knowledge to make informed financial decisions and maximize profitability.

KUMAR