Decision Tree: Risk & Opportunities

Uncertainty is a massive issue in project management and can lead to high cost and disadvantages if not handled correctly. The project manager must therefore be able to make the best decisions based on the information available.
The decision tree is a tool that can aid the project manager to ensure the best outcome of a problem.
It is based on a tree-like model where each branch is a path of decisions and possible events. Each step include the cost and possibility of that event to occur.
By identifying all the possible events and their chance to occur it gives the project manager the ability to calculate the highest probability for each path.
When combining this with the cost of each event the project manager is able to estimate the cost/benefits for each decision.

Introduction and Method Description

Decisions and uncertainties are something every project manager must be able to handle well. If not handled correctly it could lead to costly affairs. Decisions and uncertainties is something we experience almost every day. A situation where you would need to make the best decision. It could be if you are going to remodel the bathroom in your apartment and you are choosing between two contractors. Contractor A is the cheapest but is also known for having the probability of delays. Whereas contractor B costs more but have a greater chance of finishing in time. In both decisions and uncertainties are present in the terms of cost and delays. So which one do you choose? Obviously you would choose the outcome with the highest value or the one with the lowest negative impacts.
To better understand the problem let us say that contractor A will cost $35000 and with a 25 percent probability to not finish in time. Whereas contractor B will cost $50000 with a 90 percent probability of finishing in time. If either one of them fail to finish in time there would be a penalty on $10000.
Even with this small situation it can be hard to choose the best solution if no analysis of the problem is done. In larger projects there can be many decisions and uncertainties and many of them can be as a consequence of an other decision. It is therefore crucial for the project manager to have the right tools and be able to handle them. This is where the decision tree comes in handy.
The decision tree is a method to evaluate a decision making process. It is a tool that is commonly used within robotics, machine learning, statistics data mining and management. This article focus on the use within project management.

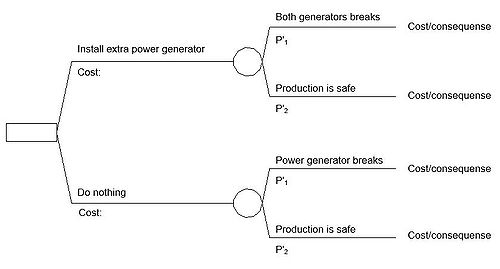
For a project manager the Bayesion decision tree analysis is used to mitigate the risk and cost of the decision. It is useful when analyzing a process that has a combination of many decisions as the user is able to calculate the effect of each decision. The decision tree is a model with three types of stages:
● A decision node (square)
● A event node (circle)
● A cost/consequence node

At the decision node the project manager has to take an active choice to move on. The event node is the effect that can happen from a choice taken. The last type of node is the cost/consequence which is the end result of decisions and events occurring.
Figure 1 shows the basic decision problem situation. It is a medicinal company that is investigating if they should install an extra power generator. If the power generator breaks down they would have to shut down production until it is fixed. A shut down could lead to massive expenses and on the same time investing in an extra power generator is also expensive. First the decision node is whether they should install the power generator or not. Both of the decisions leads to an event where there is a chance of two possible outcomes.

Figure 1. Basic decision tree

The theory behind the decision tree is to calculate the average outcome of each decision taken. In short called the Expected cost and can be expressed as this simple equation:
Expected cost = Probability of risk * Impact of the risk
E=P*I

Application of the method

Using the medicinal company's decision problem an example will be presented with the use of a Bayasian decision analysis

Decision analysis - Prior

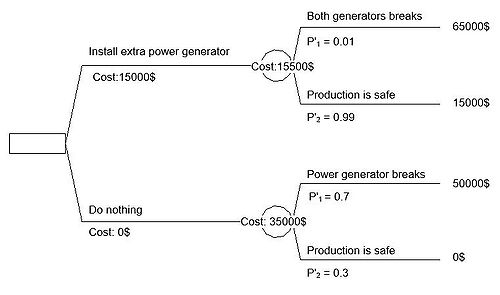
To complete the decision tree information as cost of each stage and the percentage of each event happening must be estimated. For this case the extra power generator cost 15000 $ to install and the aftereffect of the generator breaking down cost 50000 $
If no action is taken there is a 30% chance that the production is safe and 70% it is not.
By installing the generator the production has a 99% to be safe. With really bad luck there is 1% chance that both the generators break down. In the end of each branch the the expenses of each decision and events are summarized. Therefore the expense is 65000$ for the path where both generators break down as the production will get stalled as well.

Figure 2. Decision tree - Prior analysis

The expected cost can now be calculated for each branch as seen with E1 and E2
$E_1 = 0.01\cdot 65000$ + 0.99\cdot 15000$ = 15500$$
$E_2 = 0.70\cdot 50000$=35000$$
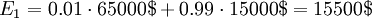
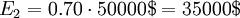
The best decision to take is then the minimum of the two expected costs. In this situation it is the path with the extra generator.

Decision analysis - Posterior

If additional information becomes available the decision tree model can be updated.
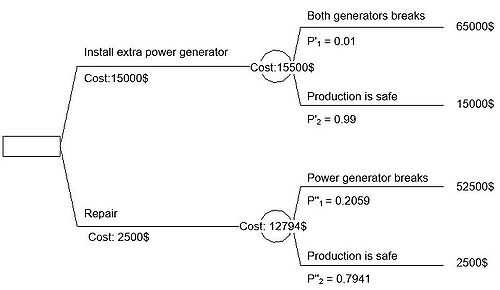
Given the same case would try to perform a repair on the current power generator.
The project manager found an external company that could do an investigation/repair on the generator for the price of 2500$. The external repair company says they have a 90% chance of fixing the problem.
The decision table is now getting additional information and the updated probability can be calculated with this equation (Bayers' rule). $P''[\theta_1|I_1] = \frac {P[I_1|\theta_1] \cdot P'[\theta_1]}{P[I_1|\theta_1] \cdot P'[\theta_1] + P[I_1|\theta_2] \cdot P'[\theta_2]}$

In the table below are the chance of a repair to be successful.

	θ2 Success	θ1 Failure
I1 Repair	0.9	0.1
I2 No repair	0.1	0.9

$P''_1 = \frac {0.1\cdot 0.7}{0.1\cdot 0.7 + 0.9\cdot 0.3}= 0.2059$
$P''_2 = \frac {0.9\cdot 0.3}{0.1\cdot 0.7 + 0.9\cdot 0.3}= 0.7941$
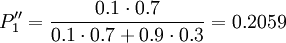
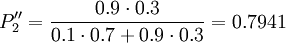
The updated probabilities are calculated and a new evaluation can be made. The estimated cost for the repaired power generator situation is then:
$E_2 = P''_1 \cdot 52500$+ P''_2 \cdot 2500$= 0.2059 \cdot 52500$+0.7941 \cdot 2500$= 12794$$
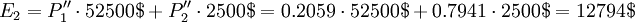
With the repair it is better to not invest in the extra generator.

Figure 3. Decision tree - Posterior analysis

Limitations

The decision tree offers many advantages when comparing to other decision making tools as it is easy to understand and simple to use. However the decision tree also has its disadvantages and limitations.

The information in the decision tree relies on precise input to provide the user with a reliable outcome. A little change in the data can result in a massive change in the outcome. Getting reliable data can be hard for the project manager for example how would you set the probability of a repair being a success or failure. Thereby the estimated cost could be way off if several events in a row has been estimated 10% wrong.
Another fundamental flaw is that the decision tree is based on expectations that will happen for each decision taken. The project managers skills to do predictions will however always be limited. There can always be unforeseen events happening from a decision taken which could change the outcome of the situation.

At the same time the decision tree is easy to use it can also be very complex and time consuming. This is seen when using it on large problems. There will be many branches and decisions which takes long time to create. With extra information added or removed the manager would probably have to re-draw the decision tree.
Having large project can easily make the tool unwieldy as it can be hard to present for colleagues if they have not been on it from the start.

Even though the decision tree seem to be easy it requires skill and expertise to master. Without this it could easily go wrong and could be at high expense for the company if the outcome was not as expected. To ensure the expertise the company would have to maintain their project managers skills which could be expensive.

Having to make a decision based on valuable information is good. However having to much information can go in both ways. The project manager can hit the "paralysis of analysis" where he got a massive challenge to process all the information which will slow down the decision making capacity. Having to much information could therefore be a burden in both cost and time on analysis.

Analysis Limitations